
6.已知函数f(x)=x2,g(x)=x-1.
(1)若存在x∈R使f(x)<b·g(x),求实数b的取值范围;
(2)设F(x)=f(x)-mg(x)+1-m-m2,且|F(x)|在[0,1]上单调递增,求实数m的取值范围.
解:(1) x∈R,f(x)<b·g(x)?x∈R,x2-bx+b<0?Δ=(-b)2-4b>0?b<0或b>4.(2)F(x)=x2-mx+1-m2,Δ=m2-4(1-m2)=5m2-4,
x∈R,f(x)<b·g(x)?x∈R,x2-bx+b<0?Δ=(-b)2-4b>0?b<0或b>4.(2)F(x)=x2-mx+1-m2,Δ=m2-4(1-m2)=5m2-4,
①当Δ≤0即-≤m≤时,则必需
?-≤m≤0.
②当Δ>0即m<-或m>时,设方程F(x)=0的根为x1,x2(x1<x2),若≥1,则x1≤0.
?m≥2.
若≤0,则x2≤0,
?-1≤m<-.综上所述:-1≤m≤0或m≥2.
B组
5.(原创题)如果对于函数f(x)定义域内任意的x,都有f(x)≥M(M为常数),称M为f(x)的下界,下界M中的最大值叫做f(x)的下确界,下列函数中,有下确界的所有函数是________.
①f(x)=sinx;②f(x)=lgx;③f(x)=ex;④f(x)=
解析:∵sinx≥-1,∴f(x)=sinx的下确界为-1,即f(x)=sinx是有下确界的函数;∵f(x)=lgx的值域为(-∞,+∞),∴f(x)=lgx没有下确界;∴f(x)=ex的值域为(0,+∞),∴f(x)=ex的下确界为0,即f(x)=ex是有下确界的函数;
∵f(x)=的下确界为-1.∴f(x)=是有下确界的函数.答案:①③④
4.已知函数f(x)=|ex+|(a∈R)在区间[0,1]上单调递增,则实数a的取值范围__.
解析:当a<0,且ex+≥0时,只需满足e0+≥0即可,则-1≤a<0;当a=0时,f(x)=|ex|=ex符合题意;当a>0时,f(x)=ex+,则满足f′(x)=ex-≥0在x∈[0,1]上恒成立.只需满足a≤(e2x)min成立即可,故a≤1,综上-1≤a≤1.
答案:-1≤a≤1
3.函数y=+ 的值域是________.
解析:令x=4+sin2α,α∈[0,],y=sinα+cosα=2sin(α+),∴1≤y≤2.
答案:[1,2]
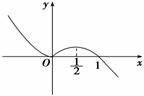
2.函数f(x)(x∈R)的图象如右图所示,则函数g(x)=f(logax)(0<a<1)的单调减区间是________.
解析:∵0<a<1,y=logax为减函数,∴logax∈[0,]时,g(x)为减函数.
由0≤logax≤?≤x≤1.答案:[,1](或(,1))
1.(2009年高考福建卷改编)下列函数f(x)中,满足“对任意x1,x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的是________.
①f(x)= ②f(x)=(x-1)2 ③f(x)=ex ④f(x)=ln(x+1)
 解析:∵对任意的x1,x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2),∴f(x)在(0,+∞)上为减函数.答案:①
解析:∵对任意的x1,x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2),∴f(x)在(0,+∞)上为减函数.答案:①
8.已知正方形的中心为直线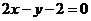 和
和 的交点,正方形一边所在直线的方程为
的交点,正方形一边所在直线的方程为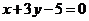 ,求其它三边所在的直线方程.
,求其它三边所在的直线方程.
7.已知三条直线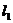 :
: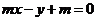 ,
,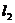 :
: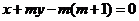 ,
,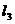 :
: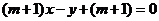 ,它们围成
,它们围成 .
.
(1)求证:不论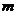 取何值时,
取何值时, 中总有一个顶点为定点;
中总有一个顶点为定点;
(2)当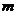 取何值时,
取何值时, 的面积取最大值、最小值?并求出最大值、最小值.
的面积取最大值、最小值?并求出最大值、最小值.
6.已知直线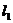 :
: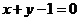 ,
,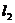 :
: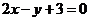 ,求直线
,求直线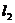 关于直线
关于直线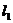 对称的直线
对称的直线 的方程.
的方程.
5.△ABC中,顶点 、
、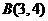 、内心
、内心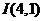 ,则顶点
,则顶点 的坐标为 .
的坐标为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com