
一般而言,高考中对冲量、动量的考查主要集中在对概念的理解和简单应用,动量定理的一般应用及对现象的解析
[真题1]一位质量为m的运动员从下蹲状态向上起跳,经Δt时间,身体伸直并刚好离开地面,速度为v.在此过程中,( )
A.地面对他的冲量为mv+mgΔt,地面对他做的功为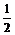 mv2
mv2
B.地面对他的冲量为mv+mgΔt,地面对他做的功为零
C.地面对他的冲量为mv,地面对他做的功为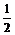 mv2
mv2
D.地面对他的冲量为mv-mgΔt,地面对他做的功为零
[解析]取运动员为研究对象,由动量定理得: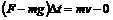 ,即
,即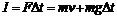 ,运动员地面没有离开地面,地面对运动员的弹力做功为零.所以B选项正确.
,运动员地面没有离开地面,地面对运动员的弹力做功为零.所以B选项正确.
[点评]本题考查了考生对冲量和功这两个概念的理解,冲量和功都是过程量,但决定因素不一样,冲量是力在时间上的积累,而功是力在空间上的积累.
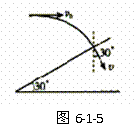 [真题2]如图6-1-5所示,一质量为m的小球,以初速度
[真题2]如图6-1-5所示,一质量为m的小球,以初速度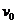 沿水平方向射出,恰好垂直地射到一倾角为300的固定斜面上,并立即反方向弹回.已知反弹速度的大小是入射速度大小的
沿水平方向射出,恰好垂直地射到一倾角为300的固定斜面上,并立即反方向弹回.已知反弹速度的大小是入射速度大小的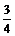 ,求在碰撞中斜面对小球的冲量大小.
,求在碰撞中斜面对小球的冲量大小.
[解析]小球在碰撞斜面前做平抛运动.设刚要碰撞斜面时小球速度为 .由题意,
.由题意, 的方向与竖直线的夹角为30°,且水平分量仍为
的方向与竖直线的夹角为30°,且水平分量仍为 0,如图.由此得
0,如图.由此得 =2
=2 0 ,碰撞过程中,小球速度由
0 ,碰撞过程中,小球速度由 变为反向的
变为反向的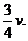 碰撞时间极短,可不计重力的冲量,由动量定理,斜面对小球的冲量为
碰撞时间极短,可不计重力的冲量,由动量定理,斜面对小球的冲量为
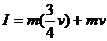 ,
,
由①、②得
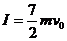
[点评]本题考查了考生应用动量定理处理变力的冲量的能力,在应用动量定理的时候一定要注意其矢量性.
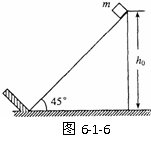 [真题3]如图6-1-6一倾角为θ=45°的斜面固定于地面,斜面顶端离地面的高度h0=1m,斜面底端有一垂直于斜而的固定挡板.在斜面顶端自由释放一质量m=0.09kg的小物块(视为质点).小物块与斜面之间的动摩擦因数μ=0.2.当小物块与挡板碰撞后,将以原速返回.重力加速度g=10 m/s2.在小物块与挡板的前4次碰撞过程中,挡板给予小物块的总冲量是多少?
[真题3]如图6-1-6一倾角为θ=45°的斜面固定于地面,斜面顶端离地面的高度h0=1m,斜面底端有一垂直于斜而的固定挡板.在斜面顶端自由释放一质量m=0.09kg的小物块(视为质点).小物块与斜面之间的动摩擦因数μ=0.2.当小物块与挡板碰撞后,将以原速返回.重力加速度g=10 m/s2.在小物块与挡板的前4次碰撞过程中,挡板给予小物块的总冲量是多少?
[解析]解法一:设小物块从高为h处由静止开始沿斜面向下运动,到达斜面底端时速度为v.
由功能关系得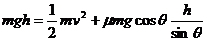 ①
①
以沿斜面向上为动量的正方向.按动量定理,碰撞过程中挡板给小物块的冲量
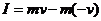 ②
②
设碰撞后小物块所能达到的最大高度为h’,则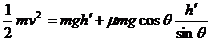 ③
③
同理,有 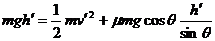 ④
④
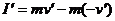 ⑤
⑤
式中,v’为小物块再次到达斜面底端时的速度,I’为再次碰撞过程中挡板给小物块的冲量.由①②③④⑤式得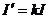 ⑥
⑥
式中 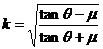 ⑦
⑦
由此可知,小物块前4次与挡板碰撞所获得的冲量成等比级数,首项为
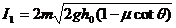 ⑧
⑧
总冲量为  ⑨
⑨
由 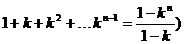 ⑩
⑩
得 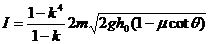 ⑾
⑾
代入数据得 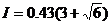 N·s
⑿
N·s
⑿
解法二:设小物块从高为h处由静止开始沿斜面向下运动,小物块受到重力,斜面对它的摩擦力和支持力,小物块向下运动的加速度为a,依牛顿第二定律得
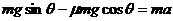 ①
①
设小物块与挡板碰撞前的速度为v,则
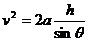 ②
②
以沿斜面向上为动量的正方向.按动量定理,碰撞过程中挡板给小物块的冲量为
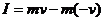 ③
③
由①②③式得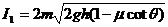 ④
④
设小物块碰撞后沿斜面向上运动的加速度大小为a’, 依牛顿第二定律有
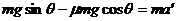 ⑤
⑤
小物块沿斜面向上运动的最大高度为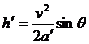 ⑥
⑥
由②⑤⑥式得 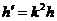 ⑦
⑦
式中 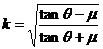 ⑧
⑧
同理,小物块再次与挡板碰撞所获得的冲量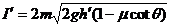 ⑨
⑨
由④⑦⑨式得 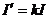 ⑩
⑩
由此可知,小物块前4次与挡板碰撞所获得的冲量成等比级数,首项为
 ⑾
⑾
总冲量为
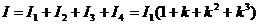 ⑿
⑿
由 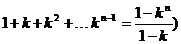 ⒀
⒀
得 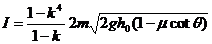 ⒁
⒁
代入数据得 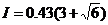 N·s
⒂
N·s
⒂
2.考点整合
考点一 动量的概念
(1)定义:物体的质量和速度的乘积叫做动量,公式:p=mv
(2)动量是描述物体运动状态的一个状态量,它与时刻相对应.
(3)动量是矢量,它的方向和速度的方向相同.
(4)动量的相对性:由于物体的速度与参考系的选取有关,所以物体的动量也与参考系选取有关,因而动量具有相对性.题中没有特别说明的,一般取地面或相对地面静止的物体为参考系.
(5)动量的变化: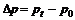 .由于动量为矢量,则求解动量的变化时,其运算遵循平行四边形定则.
.由于动量为矢量,则求解动量的变化时,其运算遵循平行四边形定则.
A、若初末动量在同一直线上,则在选定正方向的前提下,可化矢量运算为代数运算.
B、若初末动量不在同一直线上,则运算遵循平行四边形定则.
(6)动量与动能的关系: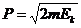 ,注意动量是矢量,动能是标量,动量改变,动能不一定改变,但动能改变动量是一定要变的.
,注意动量是矢量,动能是标量,动量改变,动能不一定改变,但动能改变动量是一定要变的.
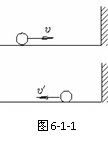 [例1]如图6-1-1一个质量是0.2kg的钢球,以2m/s的速度射到坚硬的大理石板上,立即反弹,速度大小仍为2m/s,求出钢球动量变化的大小和方向?
[例1]如图6-1-1一个质量是0.2kg的钢球,以2m/s的速度射到坚硬的大理石板上,立即反弹,速度大小仍为2m/s,求出钢球动量变化的大小和方向?
[解析]取水平向右的方向为正方向,碰撞前钢球的速度v=2m/s,
碰撞前钢球的动量为p=mv=0.2×2kg·m/s=0.4kg·m/s.
碰撞后钢球的速度为v′= -2m/s,
碰撞后钢球的动量为p′=mv′=-0.2×2kg·m/s=-0.4kg·m/s.
碰撞前后钢球动量的变化为:Δp=pˊ-p=-0.4kg·m/s-0.4 kg·m/s=-0.8 kg·m/s
且动量变化的方向向左.
[规律总结]动量是一个矢量,动量的方向和速度方向相同,所以只要物体的速度大小或方向发生变化,动量就一定发生变化.例如做匀速直线运动的物体其动量是恒量,而做匀速圆周运动的物体,由于速度方向不断在改变,即使其动量大小不变,但因其方向不断改变,所以其动量是一变量.
考点二 冲量的概念
(1)定义:力和力的作用时间的乘积叫做冲量:I=Ft
(2)冲量是描述力的时间积累效应的物理量,是过程量,它与时间相对应.
(3)冲量是矢量,它的方向由力的方向决定(不能说和力的方向相同).如果力的方向在作用时间内保持不变,那么冲量的方向就和力的方向相同.如果力的方向在不断变化,如绳子拉物体做圆周运动,则绳的拉力在时间t内的冲量,就不能说是力的方向就是冲量的方向.对于方向不断变化的力的冲量,其方向可以通过动量变化的方向间接得出.
(4)高中阶段只要求会用I=Ft计算恒力的冲量.对于变力的冲量,高中阶段只能利用动量定理通过物体的动量变化来求.
(5)要注意的是:冲量和功不同.恒力在一段时间内可能不作功,但一定有冲量.特别是力作用在静止的物体上也有冲量.
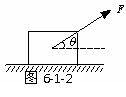 [例2]恒力F作用在质量为m的物体上,如图6-1-2所示,由于地面对物体的摩擦力较大,没有被拉动,则经时间t,下列说法正确的是( )
[例2]恒力F作用在质量为m的物体上,如图6-1-2所示,由于地面对物体的摩擦力较大,没有被拉动,则经时间t,下列说法正确的是( )
A.拉力F对物体的冲量大小为零
B.拉力F对物体的冲量大小为Ft
C.拉力F对物体的冲量大小是Ftcosθ
D.合力对物体的冲量大小为零
[解析]按照冲量的定义,物体受到恒力F作用,其冲量为Ft,物体因为静止,合外力为0,所以合力冲量为0.
[易错提示]力对物体有冲量作用必须具备力和该力作用下的时间两个条件.只要有力并且作用一段时间,那么该力对物体就有冲量作用,所以冲量是过程量.需要注意的是冲量和功不同.恒力在一段时间内可能不作功,但一定有冲量.特别是力作用在静止的物体上也有冲量.
考点三 动量定理
(1)动量定理:物体所受合外力的冲量等于物体的动量变化.既I=Δp
(2)动量定理的理解
①动量定理表明冲量是使物体动量发生变化的原因,冲量是物体动量变化的量度.这里所说的冲量必须是物体所受的合外力的冲量(或者说是物体所受各外力冲量的矢量和).
②动量定理给出了冲量(过程量)和动量变化(状态量)间的互求关系.
③现代物理学把力定义为物体动量的变化率: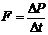 (牛顿第二定律的动量形式).
(牛顿第二定律的动量形式).
④动量定理的表达式是矢量式.在一维的情况下,各个矢量必须以同一个规定的方向为正.
遇到涉及力、时间和速度变化的问题时.运用动量定理解答往往比运用牛顿运动定律及运动学规律求解简便.应用动量定理解题的思路和一般步骤为:
(l)明确研究对象和物理过程;
(2)分析研究对象在运动过程中的受力情况;
(3)选取正方向,确定物体在运动过程中始末两状态的动量;
(4)依据动量定理列方程、求解.
[例3] 一粒钢珠从静止状态开始自由下落,然后陷人泥潭中.若把在空中下落的过程称为过程Ⅰ,进人泥潭直到停止的过程称为过程Ⅱ, 则( )
A、过程I中钢珠的动量的改变量等于重力的冲量
B、过程Ⅱ中阻力的冲量的大小等于过程I中重力的冲量的大小
C、I、Ⅱ两个过程中合外力的总冲量等于零
D、过程Ⅱ中钢珠的动量的改变量等于零
[解析]根据动量定理可知,在过程I中,钢珠从静止状态自由下落.不计空气阻力,小球所受的合外力即为重力,因此钢珠的动量的改变量等于重力的 冲量,选项A正确;过程I中阻力的冲量的大小等于过程I中重力的冲量的大小与过程Ⅱ中重力的冲量的大小之和,显然B选项不对;在I、Ⅱ两个过程中,钢珠动量的改变量各不为零.且它们大小相等、方向相反,但从整体看,钢珠动量的改变量为零,故合外力的总冲量等于零,故C选项正确,D选项错误.因此,本题的正确选项为A、C.
[规律总结]这种题本身并不难,也不复杂,但一定要认真审题.要根据题意所要求的冲量将各个外力灵活组合.若本题目给出小球自由下落的高度,可先把高度转换成时间后再用动量定理.当t1>> t2时,F>>mg.
(3)简解多过程问题.
[例4]一个质量为m=2kg的物体,在F1=8N的水平推力作用下,从静止开始沿水平 面运动了t1=5s,然后推力减小为F2=5N,方向不变,物体又运动了t2=4s后撤去外力,物体再经 过t3=6s停下来.试求物体在水平面上所受的摩擦力.
[解析]:规定推力的方向为正方向,在物体运动的整个过程中,物体的初动量P1=0,?末动量P2=O.据动量定理有: 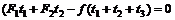 ?
?
即: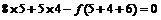 ?,解得
?,解得
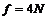 ?
?
[规律总结]由例4可知,合理选取研究过程,能简化解题步骤,提高解题速度.本题也可以用牛顿运动定律求解.同学们可比较这两种求解方法的简繁情况.
(4)求解平均力问题
[例5]质量是60kg的建筑工人,不慎从高空跌下,由于弹性安全带的保护作用,最后使人悬挂在空中.已知弹性安全带缓冲时间为1.2s,安全带伸直后长5m,求安全带所受的平均作用力.( g= 10m/s2)
[解析]人下落为自由落体运动,下落到底端时的速度为: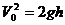
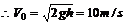
取人为研究对象,在人和安全带相互作用的过程中,人受到重力mg和安全带给的冲力 F,取F方向为正方向,由动量定理得: Ft=mV-mV0
所以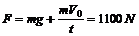 ,(方向竖直向下)
,(方向竖直向下)
[注意] 动量定理既适用于恒力作用下的问题,也适用于变力作用下的问题.如果是在变力作用下的问题,由动量定理求出的力是在t时间内的平均值.
(5)求解恒力作用下的曲线运动问题
[例6]如图6-1-3所示,以vo =10m/s2的初速度与水平方向成300角抛出一个质量m=2kg的小球.忽略空气阻力的作用,g取10m/s2.求抛出后第2s末小球速度的大小.
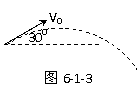
[解析]小球在运动过程中只受到重力的作用,在水平方向做匀速运动,在竖直方向做匀变速运动,竖直方向应用动量定理得:Fyt=mvy-mvy0
所以mgt=mvy-(-mv0.sin300),
解得vy=gt-v0.sin300=15m/s.而vx=v0.cos300=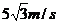
在第2s未小球的速度大小为: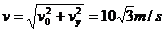
[注意]在求解曲线运动问题中,一般以动量定理的分量形式建立方程,即:Fxt=mvx-mvx0;Fyt=mvy-mvy0.
(5)求解流体问题
[例7]某种气体分子束由质量m=5.4X10-26kg速度V=460m/s的分子组成,各分子都向同一方向运动,垂直地打在某平面上后又以原速率反向弹回,如分子束中每立方米的体积内有n0=1.5X1020个分子,求被分子束撞击的平面所受到的压强.
[解析]设在△t时间内射到 S的某平面上的气体的质量为ΔM,则: 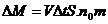
取ΔM为研究对象,受到的合外力等于平面作用到气体上的压力F以V方向规定为正方向,由动量定理得:-FΔt=ΔMV-(-ΔM.V),解得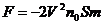 ,平面受到的压强P为:
,平面受到的压强P为: 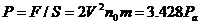
[注意]处理有关流体(如水、空气、高压燃气等)撞击物体表面产生冲力(或压强)的问题,可以说非动量定理莫属.解决这类问题的关键是选好研究对象,一般情况下选在极短时间△t内射到物体表面上的流体为研究对象
(6)对系统应用动量定理.
[例8]如图6-1-4所示, 质量为M的汽车带着质量为m的拖车在平直公路上以加速度a匀加速前进,当速度为V0时拖车突然与汽车脱钩,到拖车停下瞬间司机才发现.若汽车的牵引力一直未变,车与路面的动摩擦因数为μ,那么拖车刚停下时,汽车的瞬时速度是多大?
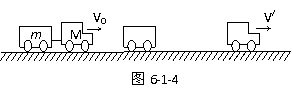
[解析]以汽车和拖车系统为研究对象,全过程系统受的合外力始终为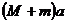 ,该过程经历时间为V0/μg,末状态拖车的动量为零.全过程对系统用动量定理可得:
,该过程经历时间为V0/μg,末状态拖车的动量为零.全过程对系统用动量定理可得:
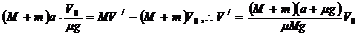
[注意]这种方法只能用在拖车停下之前.因为拖车停下后,系统受的合外力中少了拖车受到的摩擦力,因此合外力大小不再是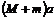 .
.
1.考纲解读
|
考纲内容 |
能力要求 |
考向定位 |
|
动量和冲量 |
理解动量的的概念,知道冲量的意义 理解动量和冲量都是矢量,会计算一维动量变化 理解动量变化和力之间的关系,会用来计算相关问题 |
考纲对冲量、动量的考查主要集中在对概念的理解和简单应用上,考纲要求为I级,动量定理在考纲中没有明确提出来,但是在教材中出现了动量定理的表达式,因此要掌握动量定理的一般应用. |


第1讲 冲量 动量 动量定理
|
碰撞与动量守恒 |
动量、动量守恒定律及其应用 弹性碰撞和非弹性碰撞 |
Ⅱ Ⅰ |
只限于一维 |
22.(本小题满分12分)
如图,已知点A、 B是椭圆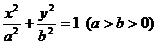 的两个顶点,若点
C(t,t)(t>0)在椭圆上,且满足
的两个顶点,若点
C(t,t)(t>0)在椭圆上,且满足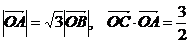 .(其中O为坐标原点)
.(其中O为坐标原点)
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线l与椭圆交于两点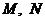 ,当
,当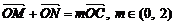 时,求
时,求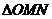 面积的最大值。
面积的最大值。

吉林市普通中学2009-2010学年度高中毕业班上学期期末教学质量检测
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com