
5.(原创题)已知定义在R上的函数f(x)是偶函数,对x∈R,f(2+x)=f(2-x),当f(-3)=-2时,f(2011)的值为________.
解析:因为定义在R上的函数f(x)是偶函数,所以f(2+x)=f(2-x)=f(x-2),故函数f(x)是以4为周期的函数,所以f(2011)=f(3+502×4)=f(3)=f(-3)=-2.答案:-2
4.(2009年高考辽宁卷改编)已知偶函数f(x)在区间[0,+∞)上单调增加,则满足f(2x-1)<f()的x取值范围是________.
解析:由于f(x)是偶函数,故f(x)=f(|x|),由f(|2x-1|)<f(),再根据f(x)的单调性得|2x-1|<,解得<x<.答案:(,)
3.(2009年高考山东卷改编)已知定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数,则f(-25)、f(11)、f(80)的大小关系为________.
解析:因为f(x)满足f(x-4)=-f(x),所以f(x-8)=f(x),所以函数是以8为周期的周期函数,则f(-25)=f(-1),f(80)=f(0),f(11)=f(3),又因为f(x)在R上是奇函数,f(0)=0,得f(80)=f(0)=0,f(-25)=f(-1)=-f(1),而由f(x-4)=-f(x)得f(11)=f(3)=-f(-3)=-f(1-4)=f(1),又因为f(x)在区间[0,2]上是增函数,所以f(1)>f(0)=0,所以-f(1)<0,即f(-25)<f(80)<f(11).
答案:f(-25)<f(80)<f(11)
2.(2010年广东三校模拟)定义在R上的函数f(x)既是奇函数又是以2为周期的周期函数,则f(1)+f(4)+f(7)等于________.
解析:f(x)为奇函数,且x∈R,所以f(0)=0,由周期为2可知,f(4)=0,f(7)=f(1),又由f(x+2)=f(x),令x=-1得f(1)=f(-1)=-f(1)⇒f(1)=0,所以f(1)+f(4)+f(7)=0.答案:0
1.设偶函数f(x)=loga|x-b|在(-∞,0)上单调递增,则f(a+1)与f(b+2)的大小关系为________.
解析:由f(x)为偶函数,知b=0,∴f(x)=loga|x|,又f(x)在(-∞,0)上单调递增,所以0<a<1,1<a+1<2,则f(x)在(0,+∞)上单调递减,所以f(a+1)>f(b+2).答案:f(a+1)>f(b+2)
6.设函数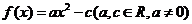 ,又
,又 ,
,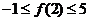 ,求
,求 的最小值、最大值以及取得最小值、最大值时
的最小值、最大值以及取得最小值、最大值时 的值.
的值.
5.已知三种食物 、
、 、
、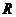 的维生素含量与成本如下表所示.
的维生素含量与成本如下表所示.
|
|
食物 |
食物 |
食物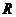 |
维生素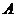 (单位/ (单位/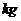 ) ) |
400 |
600 |
400 |
维生素 (单位/ (单位/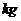 ) ) |
800 |
200 |
400 |
成本(元/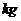 ) ) |
6 |
5 |
4 |
现在将 的食物
的食物 和
和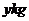 的食物
的食物 及
及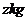 的食物
的食物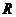 混合,制成100
混合,制成100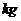 的混合物.如果这100
的混合物.如果这100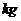 的混合物中至少含维生素
的混合物中至少含维生素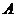 44000单位与维生素
44000单位与维生素 48000单位,那么
48000单位,那么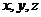 为何值时,混合物的成本最小?
为何值时,混合物的成本最小?
4.某人有楼房一幢,室内面积共180 ,拟分隔成两类房间作为旅游客房.大房间每间面积为18
,拟分隔成两类房间作为旅游客房.大房间每间面积为18 ,可住游客5名,每名游客每天住宿费为40元;小房间每间面积为15
,可住游客5名,每名游客每天住宿费为40元;小房间每间面积为15 ,可住游客3名,每名游客每天住宿费为50元.装修大房间每间需1000元,装修小房间每间需600元.如果他只能筹款8000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,能获得最大收益?
,可住游客3名,每名游客每天住宿费为50元.装修大房间每间需1000元,装修小房间每间需600元.如果他只能筹款8000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,能获得最大收益?
3.已知整点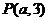 在不等式组
在不等式组 表示的平面区域内,则
表示的平面区域内,则 为
.
为
.
2.已知集合 ,集合
,集合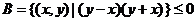 ,
,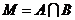 ,则
,则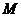 的面积是
.
的面积是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com