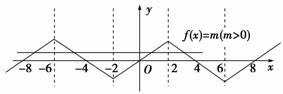
9．(2009年高考山东卷)已知定义在R上的奇函数f(x)满足f(x－4)＝－f(x)，且在区间[0,2]上是增函数．若方程f(x)＝m(m＞0)在区间[－8,8]上有四个不同的根x₁，x₂，x₃，x₄，则x₁+x₂+x₃+x₄＝________.

解析：因为定义在R上的奇函数，满足f(x－4)＝－f(x)，所以f(4－x)＝f(x)，因此，函数图象关于直线x＝2对称且f(0)＝0.由f(x－4)＝－f(x)知f(x－8)＝f(x)，所以函数是以8为周期的周期函数．又因为f(x)在区间[0,2]上是增函数，所以f(x)在区间[－2,0]上也是增函数，如图所示，那么方程f(x)＝m(m＞0)在区间[－8,8]上有四个不同的根x₁，x₂，x₃，x₄，不妨设x₁＜x₂＜x₃＜x₄.由对称性知x₁+x₂＝－12，x₃+x₄＝4，所以x₁+x₂+x₃+x₄＝－12+4＝－8. 答案：-8

8．已知函数f(x)为R上的奇函数，当x≥0时，f(x)＝x(x+1)．若f(a)＝－2，则实数a＝________.

解析：当x≥0时，f(x)＝x(x+1)>0，由f(x)为奇函数知x<0时，f(x)<0，∴a<0，f(－a)＝2，∴－a(－a+1)＝2，∴a＝2(舍)或a＝－1.答案：－1

7．(2010年安徽黄山质检)定义在R上的函数f(x)在(－∞，a]上是增函数，函数y＝f(x+a)是偶函数，当x₁<a，x₂>a，且|x₁－a|<|x₂－a|时，则f(2a－x₁)与f(x₂)的大小关系为________．

解析：∵y＝f(x+a)为偶函数，∴y＝f(x+a)的图象关于y轴对称，∴y＝f(x)的图象关于x＝a对称．又∵f(x)在(－∞，a]上是增函数，∴f(x)在[a，+∞)上是减函数．当x₁<a，x₂>a，且|x₁－a|<|x₂－a|时，有a－x₁<x₂－a，即a<2a－x₁<x₂，∴f(2a－x₁)>f(x₂)．答案：f(2a－x₁)>f(x₂)

6．(2010年江苏苏州模拟)已知函数f(x)是偶函数，并且对于定义域内任意的x，满足f(x+2)＝－，若当2<x<3时，f(x)＝x，则f(2009.5)＝________.

解析：由f(x+2)＝－，可得f(x+4)＝f(x)，f(2009.5)＝f(502×4+1.5)＝f(1.5)＝f(－2.5)∵f(x)是偶函数，∴f(2009.5)＝f(2.5)＝.答案：

5．(2009年高考江西卷改编)已知函数f(x)是(－∞，+∞)上的偶函数，若对于x≥0，都有f(x+2)＝f(x)，且当x∈[0,2)时，f(x)＝log₂(x+1)，则f(－2009)+f(2010)的值为________．

解析：∵f(x)是偶函数，∴f(－2009)＝f(2009)．∵f(x)在x≥0时f(x+2)＝f(x)，∴f(x)周期为2.∴f(－2009)+f(2010)＝f(2009)+f(2010)＝f(1)+f(0)＝log₂2+log₂1＝0+1＝1.答案：1

4．(2010年湖南郴州质检)已知函数f(x)是R上的偶函数，且在(0，+∞)上有f′(x)>0，若f(－1)＝0，那么关于x的不等式xf(x)<0的解集是________．

解析：在(0，+∞)上有f′(x)>0，则在(0，+∞)上f(x)是增函数，在(－∞，0)上是减函数，又f(x)在R上是偶函数，且f(－1)＝0，∴f(1)＝0.从而可知x∈(－∞，－1)时，f(x)>0；x∈(－1,0)时，f(x)<0；x∈(0,1)时，f(x)<0；x∈(1，+∞)时，f(x)>0.∴不等式的解集为(－∞，－1)∪(0,1)答案：(－∞，－1)∪(0,1)．

3．(2010年浙江台州模拟)已知f(x)是定义在R上的奇函数，且f(1)＝1，若将f(x)的图象向右平移一个单位后，得到一个偶函数的图象，则f(1)+f(2)+f(3)+…+f(2010)＝________.

解析：f(x)是定义在R上的奇函数，所以f(－x)＝－f(x)，将f(x)的图象向右平移一个单位后，得到一个偶函数的图象，则满足f(－2+x)＝－f(x)，即f(x+2)＝－f(x)，所以周期为4，f(1)＝1，f(2)＝f(0)＝0，f(3)＝－f(1)＝－1，f(4)＝0，所以f(1)+f(2)+f(3)+f(4)＝0，则f(1)+f(2)+f(3)+…+f(2010)＝f(4)×502+f(2)＝0.答案：0

2．已知定义在R上的函数f(x)满足f(x)＝－f(x+)，且f(－2)＝f(－1)＝－1，f(0)＝2，f(1)+f(2)+…+f(2009)+f(2010)＝________.

解析：f(x)＝－f(x+)⇒f(x+3)＝f(x)，即周期为3，由f(－2)＝f(－1)＝－1，f(0)＝2，所以f(1)＝－1，f(2)＝－1，f(3)＝2，所以f(1)+f(2)+…+f(2009)+f(2010)＝f(2008)+f(2009)+f(2010)＝f(1)+f(2)+f(3)＝0.答案：0

1．(2009年高考全国卷Ⅰ改编)函数f(x)的定义域为R，若f(x+1)与f(x－1)都是奇函数，则下列结论正确的是________．

①f(x)是偶函数　②f(x)是奇函数　③f(x)＝f(x+2)

④f(x+3)是奇函数

解析：∵f(x+1)与f(x－1)都是奇函数，∴f(－x+1)＝－f(x+1)，f(－x－1)＝－f(x－1)，∴函数f(x)关于点(1,0)，及点(－1,0)对称，函数f(x)是周期T＝2[1－(－1)]＝4的周期函数．∴f(－x－1+4)＝－f(x－1+4)，f(－x+3)＝－f(x+3)，即f(x+3)是奇函数．答案：④

6．已知函数y＝f(x)是定义在R上的周期函数，周期T＝5，函数y＝f(x)(－1≤x≤1)是奇函数，又知y＝f(x)在[0,1]上是一次函数，在[1,4]上是二次函数，且在x＝2时函数取得最小值－5.(1)证明：f(1)+f(4)＝0；(2)求y＝f(x)，x∈[1,4]的解析式；(3)求y＝f(x)在[4,9]上的解析式．

解：(1)证明：∵f(x)是以5为周期的周期函数，∴f(4)＝f(4－5)＝f(－1)，

又∵y＝f(x)(－1≤x≤1)是奇函数，∴f(1)＝－f(－1)＝－f(4)，∴f(1)+f(4)＝0.

(2)当x∈[1,4]时，由题意可设f(x)＝a(x－2)²－5(a>0)，由f(1)+f(4)＝0，得a(1－2)²－5+a(4－2)²－5＝0，∴a＝2，∴f(x)＝2(x－2)²－5(1≤x≤4)．

(3)∵y＝f(x)(－1≤x≤1)是奇函数，∴f(0)＝0，又知y＝f(x)在[0,1]上是一次函数，∴可设f(x)＝kx(0≤x≤1)，而f(1)＝2(1－2)²－5＝－3，∴k＝－3，∴当0≤x≤1时，f(x)＝－3x，从而当－1≤x<0时，f(x)＝－f(－x)＝－3x，故－1≤x≤1时，f(x)＝－3x.∴当4≤x≤6时，有－1≤x－5≤1，∴f(x)＝f(x－5)＝－3(x－5)＝－3x+15.当6<x≤9时，1<x－5≤4，∴f(x)＝f(x－5)＝2[(x－5)－2]²－5＝2(x－7)²－5.

∴f(x)＝.

B组