
18.(本小题满分12分)用0,1,2, 3,4,5这六个数字:
(1)能组成多少个无重复数字的四位偶数?
(2)能组成多少个无重复数字且为5的倍数的五位数?
(3)能组成多少个无重复数字且比1325大的四位数?
17. (本小题满分12分)已知二次函数 在
在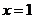 处取得极值,且在
处取得极值,且在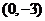 点处的切线与直线
点处的切线与直线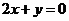 平行.
平行.
(Ⅰ)求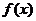 的解析式;
的解析式;
(Ⅱ)求函数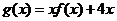 的单调递增区间.
的单调递增区间.
16.函数 的单调递增区间为 ___.
的单调递增区间为 ___.
15. 市内某公共汽车站有10个候车位(排成一排),现有4名乘客随便坐在某个座位上候车,则恰好有5个连续空座位的候车方式共有_____________种.
14.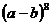 的展开式中系数最小的项等于 .
的展开式中系数最小的项等于 .
13. 若复数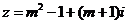 为纯虚数,则实数
为纯虚数,则实数 ____________.
____________.
12.已知直线 是
是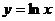 的切线,则
的切线,则 的值为
( )
的值为
( )
(A)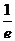 (B)
(B)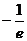 (C)
(C) (D)
(D)
11. 设有编号为1,2,3,4,5的五个茶杯和编号为1,2,3,4,5的五个杯盖,将五个杯盖盖在五个茶杯上,至少有两个杯盖和茶杯的编号相同的盖法有( )
A.30种 B.31种 C.32种 D.36种
10.  为有理数),则
为有理数),则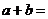 ( )
( )
A.33 B.29 C.23 D.19
9. 右图是函数 的导函数
的导函数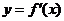 的图象,
的图象,
 给出下列命题:
给出下列命题:
①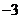 是函数
是函数 的极值点;
的极值点;
②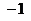 是函数
是函数 的最小值点;
的最小值点;
③ 在
在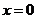 处切线的斜率小于零;
处切线的斜率小于零;
④ 在区间
在区间 上单调递增.
上单调递增.
则正确命题的序号是( )
A.①② B.①④ C.②③ D.③④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com