
2.设曲线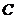 是到两坐标轴距离相等点的轨迹,那么
是到两坐标轴距离相等点的轨迹,那么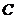 的方程是 ( )
的方程是 ( )
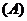
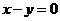
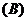
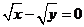
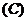
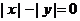
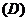
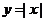 和
和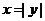
1.已知坐标满足方程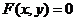 的点都在曲线
的点都在曲线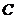 上,那么 ( )
上,那么 ( )
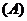
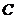 上的点的坐标都适合方程
上的点的坐标都适合方程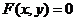 ;
;
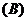 凡坐标不适合
凡坐标不适合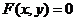 的点都不在
的点都不在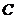 上;
上;
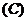 不在
不在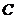 上的点的坐标必不适合
上的点的坐标必不适合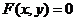 ;
;
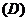 不在
不在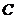 上的点的坐标有些适合
上的点的坐标有些适合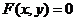 ;
;
例1.过点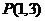 作两条相互垂直的直线
作两条相互垂直的直线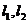 ,
,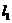 交
交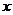 轴于
轴于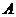 点,
点,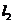 交
交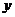 轴于
轴于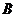 点,求线段
点,求线段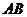 的中点
的中点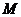 的轨迹方程。
的轨迹方程。
例2.已知点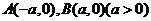 ,
,
(1)若动点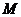 与
与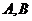 是一个直角三角形的三个顶点,求直角顶点
是一个直角三角形的三个顶点,求直角顶点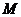 的轨迹方程;
的轨迹方程;
(2)若动点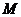 满足条件:
满足条件: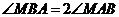 ,求点
,求点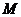 的轨迹方程.
的轨迹方程.
例3.设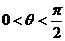 ,曲线
,曲线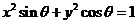 和
和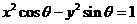 有四个交点,
有四个交点,
(1)求 的范围;(2)证明:这四个交点共圆,并求该圆半径的取值范围。
的范围;(2)证明:这四个交点共圆,并求该圆半径的取值范围。
5.若两直线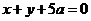 与
与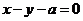 交点在曲线
交点在曲线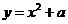 上,则
上,则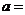 。
。
4.若直线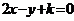 与曲线
与曲线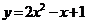 没有公共点,则
没有公共点,则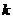 的取值范围是
。
的取值范围是
。
3.方程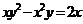 所表示的曲线是
( )
所表示的曲线是
( )
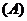 关于
关于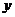 轴对称
轴对称
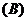 关于
关于 对称
对称
 关于原点对称
关于原点对称
 关于
关于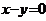 对称
对称
2.已知两点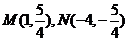 ,给出下列曲线方程:(1)
,给出下列曲线方程:(1)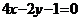 ,(2)
,(2)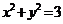 ,(3)
,(3)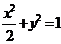 ,(4)
,(4)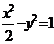 曲线上存在点
曲线上存在点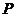 满足
满足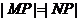 的所有曲线方程是( )
的所有曲线方程是( )
 (1)(2)(3)
(1)(2)(3)  (2)(4)
(2)(4)  (1)(3)
(1)(3)  (2)(3)(4)
(2)(3)(4)
1.设方程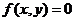 的解集非空,如果命题“坐标满足方程
的解集非空,如果命题“坐标满足方程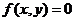 的点都在曲线
的点都在曲线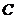 上”是不正确的,则下列命题中正确的是
( )
上”是不正确的,则下列命题中正确的是
( )
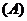 坐标满足方程
坐标满足方程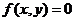 的点都不在曲线
的点都不在曲线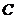 上;
上;
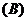 曲线
曲线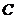 上的点的坐标都不满足方程
上的点的坐标都不满足方程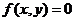 ;
;
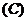 坐标满足方程
坐标满足方程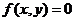 的点有些在曲线
的点有些在曲线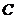 上,有些不在曲线
上,有些不在曲线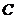 上;
上;
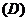 一定有不在曲线
一定有不在曲线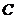 上的点,其坐标满足
上的点,其坐标满足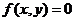 ;
;
2.求轨迹方程的常用方法:直接法、代入法、交轨法和参数法.;
1.掌握“方程曲线”的充要关系;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com