20.(2010宁夏银川一中二模)补写出下面名篇名句中的空缺部分

　 (1)后值倾覆，___________________，___________________，尔来二十有一年矣。

(《出师表》)

　 (2)____________________，娇儿恶卧踏里裂。床头屋漏无干处，_______________。

(《茅屋为秋风所破歌》)

　 (3)木直中绳，輮以为轮，其曲中规，__________________，________________，輮使之然也。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (《劝学》)

19.(辽宁丹东2009-2010学年度下高二[新高三]期末质量监测)

　 (1)　　　　　　　　　 ，　　　　　　　　　 。置杯焉则胶，水浅而舟大也。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (庄子《逍遥游》)

　 (2)青泥何盘盘，百步九折萦岩峦。　　　　　　　　　 ，　　　　　　　　　 。

(李白《蜀道难》)

　 (3)故国神游，多情应笑我，早生华发，　　　 　　　，　　　　　　　 。

(苏轼《念奴娇·赤壁怀古》)

18.(2010江苏徐州三模)补写下列名旬名篇中的空缺部分

　 (1)子曰：“　　　　　　　　　　 ，思而不学则殆。”　　　　　　　 (《论语·为政》)

　 (2)水何澹澹，　　　　　　　　　 。　　　　　　　　　　　　　　 (曹操《观沧海》)

　 (3)　　　　　　　　 ，弃脂水也；烟斜雾横，　　　　　　 。　 (杜牧《阿房宫赋》)

　 (4)若夫乘天地之正，　　　　　　 ，以游无穷者，　　　　　　 ! (庄子《逍遥游》)

　 (5)　　　　　　　　　 ，潦倒新停浊酒杯。　　　　　　　　　　　 (杜甫《登高》)

　 (6)大风起兮云飞扬，　　　　　　　　　　 ，安得猛士兮守四方!　 (刘邦《大风歌》)

17.(2010四川成都石室中学)按要求写出名流名句中的空缺部分。

　 (1)吞二周而亡诸侯，　　　　　　 ，执敲扑而鞭笞天下，威振四海。(贾谊《过秦论》)

　　　　 古代文主擅长借“梦”寄托情思，如李白《梦游天姥吟留别》中的“我欲因之梦吴越，　　　　　 ，”；李商隐《锦瑟》中的“　　 　　　，望帝春心托杜鹃”；苏轼《念奴娇·赤壁怀古》中的“人生知梦，　　　　　 ；”姜夔《扬州慢》中的“　　　　 ，青楼梦好，难赋深情。”

　 (2)吾师道也，　　　　　　　　 ？是故无贵无贱，无长无少，道之所存，师之所存也。(韩愈《师说》)

　　　　 王勃《滕王阁序》“山原旷其盈视，　　　　　　　 ”，描绘了山岭平原辽阔，河流湖泽纡回的壮丽图景；李白《蜀道难》“西当太白有鸟道，　　　　　　 ”，极写蜀道的高竣雄奇，不可攀越的险要；杜甫《登岳阳楼》“　　　　　　 ，乾坤日夜浮”，写出了洞庭湖烟波浩淼的雄伟气象；柳永《雨霖铃》“念去去，千里烟波，　　　　　　　 ”，展现了暮云浓重、楚天开阔、别后路途辽远的景象。

16.(2010北京崇文区二模)

(1)若夫日出而林霏开，　　　 ，晦明变化者，山问之朝暮也。(欧阳修《醉翁亭记》)

　 (2)若舍郑以为东道主，行李之往来，　　　　 ，君亦无所害。

(《左传·烛之武退秦师》)

　 (3)风急天高猿啸哀，　　　　　　　　　　　　 。(杜甫《登高》)。

　 (4)烟笼寒水月笼沙，　　　　　　　　　　　　 。(杜牧《泊秦淮》)

　 (5)斯是陋室，　　　　　　　　　　　 。(刘禹锡《陋室铭》)

　 (6)小楼昨夜又东风，　　　　　　　　 。(李煜《虞美人》)

　 (7)红酥手，黄滕酒，　　　　　　　　　　 。(陆游《钗头风》)

　 (8)地也，你不分好歹何为地！天也，　　　　　　　　　 ！(关汉卿《窦娥冤》)

15.(2010甘肃华亭一中五模)补写出下列名篇名句中的空缺部分。

(1)联想是回忆的一种形式。表象联想就是表象之间彼此互相引起的。“_______________，秋水共长天一色”，这是由空间上的接近而引起的联想。“故垒西边，_______________”，由历史事件发生的地点联想到有关历史人物，这是相关联想。“问君能有几多愁，_______________”，由“愁”想到江水长流，这是由特征相似引起的联想。“露从今夜白，_______________”，时令、月色，触景生情，伤心折肠，这是因果联想。《琵琶行》中的两句“_______________，_______________”,由琴声想到珠玉声，是声音的类比联想。苏轼《前赤壁赋》形容洞箫声“其声呜呜然，如怨如慕，如泣如诉，_______________ ，_______________。”这是通过音乐引起联想，运用一系列比喻描写听者的感受。

(2)岳阳楼真是幸运，有过杜甫“ _______________，_______________。”的苍凉，也有过孟浩然“_______________，_______________”的豪情。范仲淹一句“_______________ ，_______________”更为山水添色，使岳阳楼名震天下。

谢朓在《晚登三山还望京邑》中有“余霞散成绮，澄江静如练”两句，王安石在《桂枝香•金陵怀古》中就化用成了“__________________”，而“__________________”一句，则是化用自杜牧的《台城曲》中的“门外韩擒虎，楼头张丽华”。

12．(2008年高考江苏)若f₁(x)＝3^|x－p1|，f₂(x)＝2·3^|x－p2|，x∈R，p₁、p₂为常数，且

f(x)＝(1)求f(x)＝f₁(x)对所有实数x成立的充要条件(用p₁、p₂表示)；(2)设a，b是两个实数，满足a<b，且p₁、p₂∈(a，b)．若f(a)＝f(b)，求证：函数f(x)在区间[a，b]上的单调增区间的长度之和为(闭区间[m，n]的长度定义为n－m)．

解：(1)f(x)＝f₁(x)恒成立⇔f₁(x)≤f₂(x)⇔3^|x－p1|≤2·3^|x－p2|⇔3^{|x－p1|－|x－p2|}≤2

⇔|x－p₁|－|x－p₂|≤log₃2.(*)若p₁＝p₂，则(*)⇔0≤log₃2，显然成立；若p₁≠p₂，记g(x)＝|x－p₁|－|x－p₂|，当p₁>p₂时，g(x)＝

所以g(x)_max＝p₁－p₂，故只需p₁－p₂≤log₃2.

当p₁<p₂时，g(x)＝所以g(x)_max＝p₂－p₁，故只需p₂－p₁≤log₃2.

综上所述，f(x)＝f₁(x)对所有实数x成立的充要条件是|p₁－p₂|≤log₃2.

(2)证明：分两种情形讨论．

①当|p₁－p₂|≤log₃2时，由(1)知f(x)＝f₁(x)(对所有实数x∈[a，b])，则由f(a)＝f(b)及a<p₁<b易知p₁＝.再由f₁(x)＝的单调性可知，f(x)在区间[a，b]上的单调增区间的长度为b－＝.

②当|p₁－p₂|>log₃2时，不妨设p₁<p₂，则p₂－p₁>log₃2.于是，当x≤p₁时，有f₁(x)＝3^p1－x<3^p2－x<f₂(x)，从而f(x)＝f₁(x)．

当x≥p₂时，f₁(x)＝3^x－p1＝3^p2－p1·3^x－p2>3^log₃²·3^x－p2＝f₂(x)，从而f(x)＝f₂(x)．

当p₁<x<p₂时，f₁(x)＝3^x－p1及f₂(x)＝2·3^p₂^－x，由方程3^x₀^－p₁＝2·3^p₂^－x₀，解得f₁(x)与f₂(x)图象交点的横坐标为x₀＝+log₃2.①

显然p₁<x₀＝p₂－[(p₂－p₁)－log₃2]<p₂，这表明x₀在p₁与p₂之间．

由①易知f(x)＝

综上可知，在区间[a，b]上，f(x)＝

故由函数f₁(x)与f₂(x)的单调性可知，f(x)在区间[a，b]上的单调增区间的长度之和为(x₀－p₁)+(b－p₂)，由于f(a)＝f(b)，即3^p₁^－a＝2·3^b－p₂，得

p₁+p₂＝a+b+log₃2.②

故由①②得(x₀－p₁)+(b－p₂)＝b－(p₁+p₂－log₃2)＝.

11．已知函数f(x)＝.(1)求证：f(x)的图象关于点M(a，－1)对称；

(2)若f(x)≥－2^x在x≥a上恒成立，求实数a的取值范围．

解：(1)证明：设f(x)的图象C上任一点为P(x，y)，则y＝－，

P(x，y)关于点M(a，－1)的对称点为P′(2a－x，－2－y)．

∴－2－y＝－2+＝＝＝，

说明点P′(2a－x，－2－y)也在函数y＝的图象上，由点P的任意性知，f(x)的图象关于点M(a，－1)对称．

(2)由f(x)≥－2^x得≥－2^x，则≤2^x，化为2^x－a·2^x+2^x－2≥0，则有(2^x)²+2^a·2^x－2·2^a≥0在x≥a上恒成立．令g(t)＝t²+2^a·t－2·2^a，则有g(t)≥0在t≥2^a上恒成立．∵g(t)的对称轴在t＝0的左侧，∴g(t)在t≥2^a上为增函数．

∴g(2^a)≥0.∴(2^a)²+(2^a)²－2·2^a≥0，∴2^a(2^a－1)≥0，则a≥0.即实数a的取值范围为a≥0.

10．(2010年宁夏银川模拟)已知函数f(x)＝a^2x+2a^x－1(a>0，且a≠1)在区间[－1,1]上的最大值为14，求实数a的值．

解：f(x)＝a^2x+2a^x－1＝(a^x+1)²－2，∵x∈[－1,1]，

(1)当0<a<1时，a≤a^x≤，∴当a^x＝时，f(x)取得最大值．

∴(+1)²－2＝14，∴＝3，∴a＝.

(2)当a>1时，≤a^x≤a，∴当a^x＝a时，f(x)取得最大值．

∴(a+1)²－2＝14，∴a＝3.综上可知，实数a的值为或3.

9．函数y＝2^|x|的定义域为[a，b]，值域为[1,16]，当a变动时，函数b＝g(a)的图象可以是________．

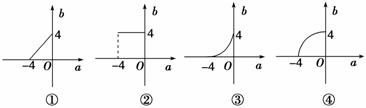
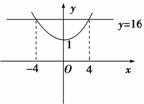解析：函数y＝2^|x|的图象如图．

当a＝－4时，0≤b≤4，

当b＝4时，－4≤a≤0，答案：②