
(三)解不等式:
例3. 设函数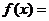
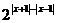 ,求使
,求使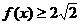 的
的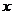 的取值范围.
的取值范围.
(1)∵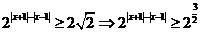 ,∴
,∴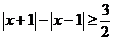
不等式等价化为①当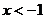 时
时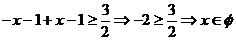
②当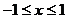 时,
时,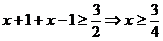
③当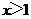 时,
时,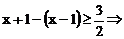 恒成立
恒成立
原不等式的解集为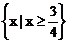
(二)求最值:
例2. (重庆理7)若a是1+2b与1-2b的等比中项,则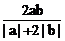 的最大值为( )
的最大值为( )
A.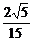 B.
B.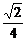 C.
C. D.
D.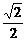
答案:B
分析:a是1+2b与1-2b的等比中项,则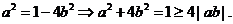

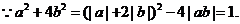
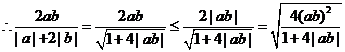
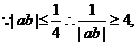
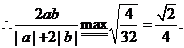
(一)基础训练题
例1.
(1)(全国2文4)下列四个数中最大的是( )
A. 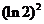 B.
B.
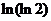 C.
C.
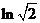 D.
D.
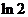
解:∵ 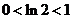 ,∴ ln(ln2)<0,(ln2)2< ln2,而ln
,∴ ln(ln2)<0,(ln2)2< ln2,而ln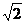 =
=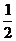 ln2<ln2,∴ 最大的数是ln2,选D。
ln2<ln2,∴ 最大的数是ln2,选D。
(2)(安徽文8)设a>1,且 ,则
,则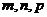 的大小关系为 ( )
的大小关系为 ( )
A. n>m>p B. m>p>n C. m>n>p D. p>m>n
解析:设a>1,∴ 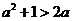 ,
,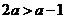 ,
,
 ,∴
,∴ 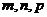 的大小关系为m>p>n,选B。
的大小关系为m>p>n,选B。
(3)(北京理7)如果正数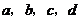 满足
满足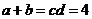 ,那么( )
,那么( )
A. 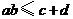 ,且等号成立时
,且等号成立时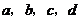 的取值唯一
的取值唯一
B. 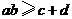 ,且等号成立时
,且等号成立时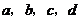 的取值唯一
的取值唯一
C. 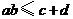 ,且等号成立时
,且等号成立时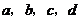 的取值不唯一
的取值不唯一
D. 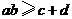 ,且等号成立时
,且等号成立时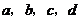 的取值不唯一
的取值不唯一
解析:正数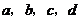 满足
满足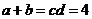 ,∴ 4=
,∴ 4=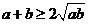 ,即
,即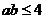 ,当且仅当a=b=2时,“=”成立;又4=
,当且仅当a=b=2时,“=”成立;又4=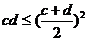 ,∴ c+d≥4,当且仅当c=d=2时,“=”成立;综上得
,∴ c+d≥4,当且仅当c=d=2时,“=”成立;综上得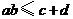 ,且等号成立时
,且等号成立时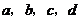 的取值都为2,选A。
的取值都为2,选A。
(4)(安徽理3)若对任意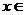 R,不等式
R,不等式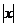 ≥ax恒成立,则实数a的取值范围是(
)
≥ax恒成立,则实数a的取值范围是(
)
A. a<-1 B.
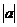 ≤1 C.
≤1 C.
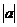 <1 D.
a≥1
<1 D.
a≥1
解析:若对任意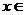 R,不等式
R,不等式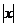 ≥ax恒成立,当x≥0时,x≥ax,a≤1,当x<0时,-x≥ax,∴a≥-1,综上得
≥ax恒成立,当x≥0时,x≥ax,a≤1,当x<0时,-x≥ax,∴a≥-1,综上得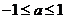 ,即实数a的取值范围是
,即实数a的取值范围是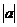 ≤1,选B。
≤1,选B。
(5)(山东文14)函数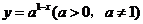 的图象恒过定点
的图象恒过定点 ,若点
,若点 在直线
在直线
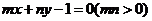 上,则
上,则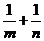 的最小值为 .
的最小值为 .
答案:4
分析:函数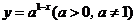 的图象恒过定点
的图象恒过定点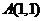 ,
,
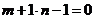 ,
,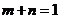 ,
,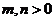 ,
,
(方法一):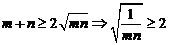 ,
, 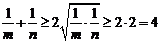 .
.
(方法二):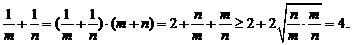
(6)(山东文15)当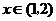 时,不等式
时,不等式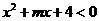 恒成立,则
恒成立,则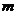 的取值范围是 .
的取值范围是 .
答案: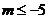
分析:构造函数: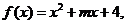
 。由于当
。由于当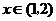 时,
时,
不等式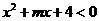 恒成立。则
恒成立。则 ,即
,即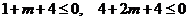 。解得:
。解得: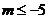 。
。
(7)(2006年重庆卷)若a, b, c>0且a(a+ b+ c)+b c=4-2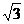 ,则2a+b+c的最小值为 ( )
,则2a+b+c的最小值为 ( )
A. 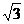 -1 B.
-1 B.
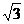 +1 C.
2
+1 C.
2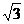 +2 D.
2
+2 D.
2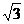 -2
-2
答案: D
1、不等式的功能:不等式的知识已渗透到函数、三角、数列、解析几何、立体几何等内容中,体现了不等式广泛运用的工具功能。
2、建立不等式的途径:运用不等式知识解题的关键是建立不等关系,其途径有:利用几何意义、利用判别式、应用变量的有界性、应用函数的有界性、应用均值不等式。
3、实际应用:应用题中有一类是最优化结果,通常是把问题转化为不等式模型,再求出最值。
[典型例题]
不等式与函数,方程,数列,导数等知识的联系。
教学难点:
不等式与几何知识的综合。
不等式的综合应用
18.(10分) 已知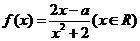 在区间
在区间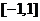 上是增函数。
上是增函数。
(Ⅰ)求实数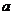 的值所组成的集合
的值所组成的集合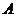 ;
;
(Ⅱ)设关于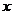 的方程
的方程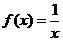
 的两个根为
的两个根为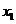 、
、 ,若对任意
,若对任意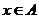 及
及 ,不等式
,不等式
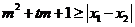 恒成立,求
恒成立,求 的取值范围.
的取值范围.
17.(本小题满分10分) 围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
16. 甲、乙两地相距S(千米),汽车从甲地匀速行驶到乙地,速度最大不得超过c(千米/小时).已知汽车每小时的运输成本(元)由可变部分与固定部分组成.可变部分与速度v(千米/小时)的平方成正比,且比例系数为正常数b;固定部分为a元.
(1)
试将全程 运输成本Y(元)表示成速度V(千米/小时)的函数.
运输成本Y(元)表示成速度V(千米/小时)的函数.
(2) 为使全程运输成本最省,汽车应以多大速度行驶?
15.
已知实数x、y满足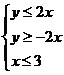 则目标函数z=x-2y的最小值是___________.
则目标函数z=x-2y的最小值是___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com