
8. 如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成”函数.给出下列函数:
①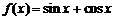 ;②
;② ;③
;③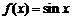 ;④
;④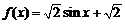 其中“互为生成”函数的是
A.①② B.②③ C.③④ D.①④
其中“互为生成”函数的是
A.①② B.②③ C.③④ D.①④
7. 已知函数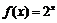 的反函数
的反函数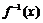 满足
满足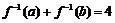 ,则
,则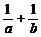 的最小值为
A.1 B.
的最小值为
A.1 B.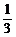 C.
C.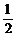 D.
D.
6. 以下四个命题中的假命题是
A.“直线a、b是异面直线”的必要不充分条件是“直线a、b不相交”
B.两直线“a∥b”的充要条件是“直线a、b与同一平面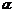 所成角相等”
C.直线“a⊥b”的充分不必要条件是“a垂直于b所在的平面”
D.“直线a∥平面
所成角相等”
C.直线“a⊥b”的充分不必要条件是“a垂直于b所在的平面”
D.“直线a∥平面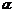 ”的必要不充分条件是“直线a平行于平面
”的必要不充分条件是“直线a平行于平面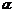 内的一条直线”
内的一条直线”
5. 某班要从6名同学中选4人参加校运会的4×100m接力比赛,其中甲、乙两名运动员必须入选,而且甲、乙两人中必须有一个人跑最后一棒,则不同的安排方法共有 A.24种 B.72种 C.144种 D.360种
4. 偶函数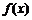 在区间[0,a] (a
> 0)上是单调函数,且满足
在区间[0,a] (a
> 0)上是单调函数,且满足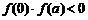 ,则方程
,则方程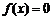 在区间[-a,a]内根的个数是
A.0 B.1 C.2 D.3
在区间[-a,a]内根的个数是
A.0 B.1 C.2 D.3
3. 抛物线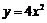 的焦点坐标为
A.(1,0) B.(0,
的焦点坐标为
A.(1,0) B.(0,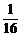 ) C.(0,1) D.(
) C.(0,1) D.(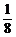 ,0)
,0)
2. 圆心为(0,4),且过点(3,0)的圆的方程为
A.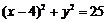 B.
B.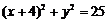 C.
C.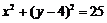 D.
D.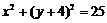
1. 设集合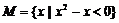 ,
,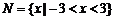 ,则
A.
,则
A.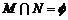 B.
B.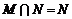 C.
C.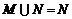 D.
D.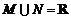
10.设函数f(x)=x2+2bx+c(c<b<1),f(1)=0,方程f(x)+1=0有实根.
(1)证明:-3<c≤-1且b≥0;
(2)若m是方程f(x)+1=0的一个实根,判断f(m-4)的正负并加以证明.
解:(1)证明:f(1)=0⇒1+2b+c=0⇒b=-.又c<b<1,故c<-<1⇒-3<c<-.方程f(x)+1=0有实根,即x2+2bx+c+1=0有实根,故Δ=4b2-4(c+1)≥0,即(c+1)2-4(c+1)≥0⇒c≥3或c≤-1.又c<b<1,得-3<c≤-1,
由b=-知b≥0.
(2)f(x)=x2+2bx+c=x2-(c+1)x+c=(x-c)(x-1),f(m)=-1<0,
∴c<m<1,∴c-4<m-4<-3<c,∴f(m-4)=(m-4-c)(m-4-1)>0,
9.(2010年湖南长沙质检)对于区间[a,b]上有意义的两个函数f(x)与g(x),如果对于区间[a,b]中的任意数x均有|f(x)-g(x)|≤1,则称函数f(x)与g(x)在区间[a,b]上是密切函数,[a,b]称为密切区间.若m(x)=x2-3x+4与n(x)=2x-3在某个区间上是“密切函数”,则它的一个密切区间可能是________.
①[3,4] ②[2,4] ③[2,3] ④[1,4]
解析:|m(x)-n(x)|≤1⇒|x2-5x+7|≤1,解此绝对值不等式得2≤x≤3,故在区间[2,3]上|m(x)-n(x)|的值域为[0,1],∴|m(x)-n(x)|≤1在[2,3]上恒成立.
答案:③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com