
15. 解:(1)令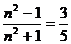 解得n=2, ∴
解得n=2, ∴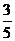 是数列中第2项。
是数列中第2项。
令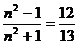 解得n=5, ∴
解得n=5, ∴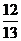 是数列中第5项。
是数列中第5项。
(2)令n=11,
令n=25, 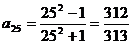 。
。
∴ 分别为
分别为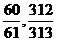 。
。
14. 2600 提示:由数列的递推公式 可知,数列的各奇数项全相等,且等于1,因此
可知,数列的各奇数项全相等,且等于1,因此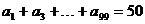 ,又数列的偶数项组成一个以2为公差的等差数列,∵
,又数列的偶数项组成一个以2为公差的等差数列,∵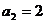 ,∴
,∴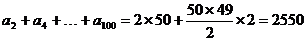 ∴
∴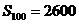 。
。
13. 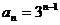 提示:n≥2时,用
提示:n≥2时,用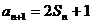 与
与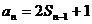 两式相减,可得
两式相减,可得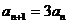 ,又知
,又知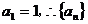 是以1为首项,3为公比的等比数列。
是以1为首项,3为公比的等比数列。
12. 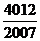 提示:
提示: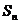
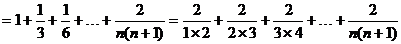
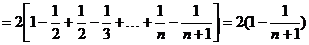 ,将n=2006代入即可。
,将n=2006代入即可。
11. 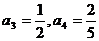 提示:依递推关系式,分别代入n=3,n=4即可。
提示:依递推关系式,分别代入n=3,n=4即可。
10. 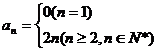 提示:令n=1,得
提示:令n=1,得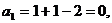 令n≥2
令n≥2
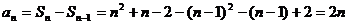 。
。
9. 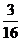
8.B 提示:由已知可得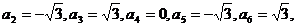 …所以
…所以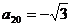 。
。
7. A 提示:因为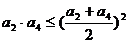 ,而
,而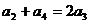 ,所以
,所以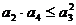
6. A 提示:由已知对任意正整数m,n都有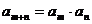 ,所以令m=n=1,得
,所以令m=n=1,得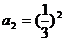 ,令m=1,n=2得
,令m=1,n=2得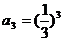 …,由此可知
…,由此可知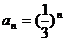 ,所以
,所以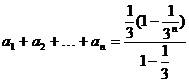 ,所以
,所以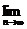 (
(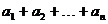 )=
)=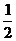 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com