25．如图9，在Rt△ABC中，∠ACB＝90°.半径为1的圆A与边AB相交于点D，与边AC相交于点E，连结DE并延长，与线段BC的延长线交于点P.

(1)当∠B＝30°时，连结AP，若△AEP与△BDP相似，求CE的长；

(2)若CE=2，BD=BC，求∠BPD的正切值；

(3)若，设CE=x，△ABC的周长为y，求y关于x的函数关系式.

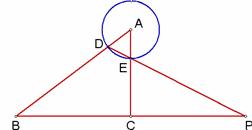
图9　　　　　　　 　　　　　　　　图10(备用)　　　　　　　　 　　　　　　图11(备用)

(1)解：∵∠B＝30°∠ACB＝90°∴∠BAC＝60°

∵AD=AE　 ∴∠AED＝60°=∠CEP

∴∠EPC＝30°

∴三角形BDP为等腰三角形

∵△AEP与△BDP相似

∴∠EAP=∠EPA=∠DBP=∠DPB=30°

∴AE=EP=1

∴在RT△ECP中，EC=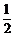EP=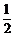

(2)过点D作DQ⊥AC于点Q，且设AQ=a，BD=x

∵AE=1,EC=2

∴QC=3-a

∵∠ACB＝90°

∴△ADQ与△ABC相似

∴

即，∴

∵在RT△ADQ中

∵

∴

解之得x=4，即BC=4

过点C作CF//DP

∴△ADE与△AFC相似，

∴，即AF=AC，即DF=EC=2,

∴BF=DF=2

∵△BFC与△BDP相似

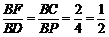∴，即：BC=CP=4

∴tan∠BPD=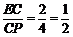

(3)过D点作DQ⊥AC于点Q，则△DQE与△PCE相似,设AQ=a，则QE=1-a

∴且

∴

∵在Rt△ADQ中，据勾股定理得：

即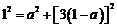：，解之得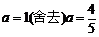

∵△ADQ与△ABC相似

∴

∴

∴三角形ABC的周长

即：，其中x>0

24．如图8，已知平面直角坐标系xOy，抛物线y＝－x²+bx+c过点A(4,0)、B(1,3) .

(1)求该抛物线的表达式，并写出该抛物线的对称轴和顶点坐标；

(2)记该抛物线的对称轴为直线l，设抛物线上的点P(m,n)在第四象限，点P关于直线l的对称点为E，点E关于y轴的对称点为F，若四边形OAPF的面积为20，求m、n的值.

(1)解：将A(4,0)、B(1,3)两点坐标代入抛物线的方程得：

解之得：b=4，c=0

所以抛物线的表达式为：

将抛物线的表达式配方得：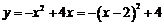

所以对称轴为x=2，顶点坐标为(2，4)

(2)点p(m，n)关于直线x=2的对称点坐标为点E(4-m，n)，则点E关于y轴对称点为点F坐标为(4-m,-n)，

则四边形OAPF可以分为：三角形OFA与三角形OAP，则

= + = =20

所以=5，因为点P为第四象限的点，所以n<0，所以n= -5

代入抛物线方程得m=5

23．已知梯形ABCD中，AD//BC，AB=AD(如图7所示)，∠BAD的平分线AE交BC于点E，连结DE.

(1)在图7中，用尺规作∠BAD的平分线AE(保留作图痕迹，不写作法)，并证明四边形ABED是菱形；

(2)∠ABC＝60°，EC=2BE，求证：ED⊥DC.

(1)解：分别以点B、D为圆心，以大于AB的长度为半径，分别作弧，且两弧交于一点P，则连接AP，即AP即为∠BAD的平分线，且AP交BC于点E，

∵AB=AD，∴△ABO≌△AOD　 ∴BO=OD

∵AD//BC, ∴∠OBE=∠ODA, ∠OAD=OEB

∴△BOE≌△DOA

∴BE=AD(平行且相等)

∴四边形ABDE为平行四边形，另AB=AD，

∴四边形ADBE为菱形

(2)设DE=2a,则CE=4a，过点D作DF⊥BC

∵∠ABC＝60°，∴∠DEF=60°, ∴∠EDF=30°, ∴EF=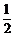DE=a，则DF=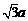，CF=CE-EF=4a-a=3a，

∴

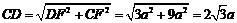
∴DE=2a，EC=4a,CD=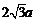,构成一组勾股数，

∴△EDC为直角三角形，则ED⊥DC

22.某环保小组为了解世博园的游客在园区内购买瓶装饮料

数量的情况，一天，他们分别在A、B、C三个出口处，

对离开园区的游客进行调查，其中在A出口调查所得的

数据整理后绘成图6.

(1)在A出口的被调查游客中，购买2瓶及2瓶以上饮料

的游客人数占A出口的被调查游客人数的___60____%.

(2)试问A出口的被调查游客在园区内人均购买了多少瓶饮料？

(3)已知B、C两个出口的被调查游客在园区内人均购买饮料

的数量如表一所示 若C出口的被调查人数比B出口的被

调查人数多2万，且B、C两个出口的被调查游客在园区

内共购买了49万瓶饮料，试问B出口的被调查游客人数

为多少万？

　　　 9万

解：(1)由图6知，购买2瓶及2瓶以上饮料的游客人数为2.5+2+1.5=6(万人)

而总人数为：1+3+2.5+2+1.5=10(万人)

所以购买2瓶及2瓶以上饮料的游客人数占A出口的被调查游客人数的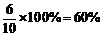

(2)购买饮料总数位：3×1+2.5×2+2×3+1.5×4=3+5+6+6=20(万瓶)

人均购买=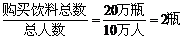

(3)设B出口人数为x万人，则C出口人数为(x+2)万人

则有3x+2(x+2)=49

解之得x=9

所以设B出口游客人数为9万人

21.机器人“海宝”在某圆形区域表演“按指令行走”，如图5所示，“海宝”从圆心O出发，先沿北偏西67.4°方向行走13米至点A处，再沿正南方向行走14米至点B处，最后沿正东方向行走至点C处，点B、C都在圆O上.(1)求弦BC的长；(2)求圆O的半径长.

(本题参考数据：sin 67.4° = ，cos 67.4° = ，tan 67.4° = )

(1)解：过点O作OD⊥AB，则∠AOD+∠AON=,即：sin∠AOD=cos∠AON=

即：AD=AO×=5,OD=AO×sin 67.4° =AO× =12

　　　　 又沿正南方向行走14米至点B处，最后沿正东方向行走至点C处

所以AB∥NS,AB⊥BC,所以E点位BC的中点，且BE=DO=12

　　　　 所以BC=24

(2)解：连接OB，则OE=BD=AB-AD=14-5=9

又在RT△BOE中，BE=12,

　　　　 所以

　　　　 即圆O的半径长为15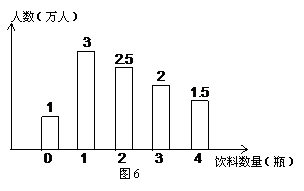

20.解方程：─ ─ 1 = 0

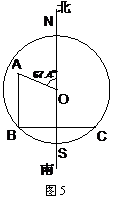解：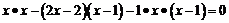

∴

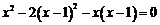
代入检验得符合要求

19.计算：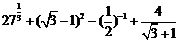　　　　　　　　　　

解：原式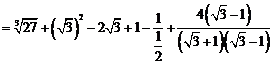　　　　

18.已知正方形ABCD中，点E在边DC上，DE = 2，EC = 1(如图4所示) 把线段AE绕点A旋转，使点E落在直线BC上的点F处，则F、C两点的距离为__1或5_________.

[解析]题目里只说“旋转”，并没有说顺时针还是逆时针，而且说的是“直线BC上的点”，所以有两种情况如图所示：

顺时针旋转得到点，则C=1

逆时针旋转得到点，则,

17.一辆汽车在行驶过程中，路程 y(千米)与时间 x(小时)之间的函数关系如图3所示 当时 0≤x≤1，y关于x的函数解析式为 y = 60 x，那么当 1≤x≤2时，y关于x的函数解析式为_____y=100x-40___.

[解析]在0≤x≤1时，把x=1代入y = 60 x，则y=60，那么当 1≤x≤2时由两点坐标(1,60)与(2,160)得当1≤x≤2时的函数解析式为y=100x-40

16.如图2，△ABC中，点D在边AB上，满足∠ACD =∠ABC，若AC = 2，AD = 1，则DB = __3________.

[解析]由于∠ACD =∠ABC，∠BAC =∠CAD,所以△ADC∽△ACB，即：,所以，则AB=4,所以BD=AB-AD=3