
3.已知函数f(x)=x+log2x,则f(x)在[,2]内的零点的个数是______.
解析:易知g(x)=x与h(x)=log2x均为增函数,故函数f(x)为增函数,且f(2)·f()<0,故函数有且只有一个零点.答案:1
2.(2010年安徽省江南十校模拟)函数f(x)=2x+x-7的零点所在的区间是____.
①(0,1) ②(1,2) ③(2,3) ④(3,4)
解析:因为f(0)=-6<0,f(1)=2+1-7=-4<0,f(2)=22+2-7=-1<0,f(3)=23+3-7=4>0,所以函数的零点在区间(2,3)内.答案:③
1.(2010年浙江温州质检)某学校开展研究性学习活动,一组同学获得了下面的一组试验数据:
|
x |
1.99 |
3 |
4 |
5.1 |
6.12 |
|
y |
1.5 |
4.04 |
7.5 |
12 |
18.01 |
现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是________
①y=2x-2 ②y=()x ③y=log2x ④y=(x2-1)
解析:代入点(2,1.5),(3,4)检验.答案:④
6.(2009年高考上海卷)有时可用函数f(x)=
描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(x∈N*),f(x)表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1)证明:当x≥7时,掌握程度的增长量f(x+1)-f(x)总是下降;
(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为(115,121],(121,127],(127,133].当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
解:(1)证明:当x≥7时,f(x+1)-f(x)=.而当x≥7时,函数y=(x-3)(x-4)单调递增,且(x-3)(x-4)>0,故f(x+1)-f(x)单调递减.
∴当x≥7,掌握程度的增长量f(x+1)-f(x)总是下降.
(2)由题意可知0.1+15ln=0.85,整理得=e0.05,
解得a=·6≈20.50×6=123.0,123.0∈(121,127].
由此可知,该学科是乙学科.
B组
5.(原创题)已知f(x)=|x|+|x-1|,若g(x)=f(x)-a的零点个数不为0,则a的最小值为________.
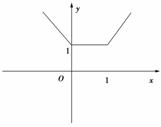
解析:作f(x)的图象,如图,g(x)=f(x)-a=0,即f(x)=a,当a=1时,g(x)有无数个零点;当a>1时,g(x)有2个零点;∴a的最小值为1.答案:1
4.(2009年高考浙江卷)某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下:
|
高峰时间段用电价格表 |
低谷时间段用电价格表 |
|
||
|
高峰月用电量 (单位:千瓦时) |
高峰电价 (单位:元/千瓦时) |
低谷月用电量 (单位:千瓦时) |
低谷电价 (单位:元/千瓦时) |
|
|
50及以下的部分 |
0.568 |
50及以下的部分 |
0.288 |
|
|
超过50至200的部分 |
0.598 |
超过50至200的部分 |
0.318 |
|
|
超过200的部分 |
0.668 |
超过200的部分 |
0.388 |
若某家庭5月份的高峰时间段用电量为200千瓦时,低谷时间段用电量为100千瓦时,则按这种计费方式该家庭本月应付的电费为________元
解析:高峰时段电费a=50×0.568+(200-50)×0.598=118.1(元).
低谷时段电费b=50×0.288+(100-50)×0.318=30.3(元).
故该家庭本月应付的电费为a+b=148.4(元).答案:148.4
3.偶函数f(x)在区间[0,a](a>0)上是单调函数,且f(0)·f(a)<0,则方程f(x)=0在区间[-a,a]内根的个数是__________.
解析:由题意函数f(x)在区间[0,a](a>0)上是单调函数,且f(0)·f(a)<0,根据零点存在定理知:在区间[0,a]内函数f(x)一定存在惟一零点且f(0)≠0,又函数f(x)是偶函数,故其在[-a,0]也惟一存在一个零点,所以方程f(x)=0在区间[-a,a]内根的个数为2.答案:2
2.根据表格中的数据,可以判定方程ex-x-2=0的一个根所在的区间为___.
|
x |
-1 |
0 |
1 |
2 |
3 |
|
ex |
0.37 |
1 |
2.72 |
7.39 |
20.09 |
|
x+2 |
1 |
2 |
3 |
4 |
5 |
解析:据题意令f(x)=ex-x-2,由于f(1)=e1-1-2=2.72-3<0,f(2)=e2-4=7.39-4>0,故函数在区间(1,2)内存在零点,即方程在相应区间内有根.
答案:(1,2)
1.已知函数f(x)=则函数f(x)的零点个数为________.
解析:只要画出分段函数的图象,就可以知道图象与x轴有三个交点,即函数的零点有3个.答案:3
10.已知双曲线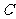 的两个焦点为
的两个焦点为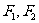 ,实半轴长与虚半轴长的乘积为
,实半轴长与虚半轴长的乘积为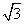 ,直线
,直线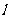 过点
过点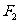 ,且与线段
,且与线段 的夹角为
的夹角为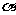 ,
,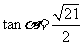 ,直线
,直线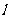 与线段
与线段 的垂直平分线的交点为
的垂直平分线的交点为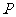 ,线段
,线段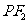 与双曲线的交点为
与双曲线的交点为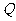 ,且
,且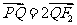 ,求双曲线方程.
,求双曲线方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com