
9、解含参数的不等式的通法是“定义域为前提,函数增减性为基础,分类讨论是关键.”如解不等式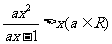 (答:
(答: 时,
时,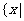
 ;
;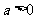 时,
时, 或
或 ;
;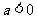 时,
时,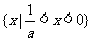 或
或 )
)
8、在解含有参数的不等式时,怎样进行讨论?(特别是指数和对数的底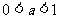 或
或 )讨论完之后,要写出:综上所述,原不等式的解是…….①
)讨论完之后,要写出:综上所述,原不等式的解是…….①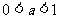 时……②
时……② 时……
时……
7、利用重要不等式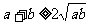 以及变式
以及变式 等求函数的最值时,你是否注意到a,b
等求函数的最值时,你是否注意到a,b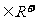 (或a ,b非负),且“等号成立”时的条件?积ab或和a+b其中之一应是定值?注意:①一正二定三取等;②积定和最小,和定积最大。常用的方法为:拆、凑、平方;如:①函数
(或a ,b非负),且“等号成立”时的条件?积ab或和a+b其中之一应是定值?注意:①一正二定三取等;②积定和最小,和定积最大。常用的方法为:拆、凑、平方;如:①函数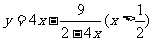 的最小值
。(答:8)②若若
的最小值
。(答:8)②若若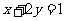 ,则
,则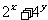 的最小值是______(答:
的最小值是______(答: );③正数
);③正数 满足
满足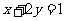 ,则
,则 的最小值为______(答:
的最小值为______(答: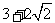 );
);
6、解指对不等式应该注意什么问题?(指数函数与对数函数的单调性, 对数的真数大于零.)含有两个绝对值的不等式如何去绝对值?(两边平方或分类讨论)
5、解分式不等式 应注意什么问题?(不能去分母,而要移项通分)。解分式不等式 的一般思路是
的一般思路是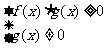
4、简单线性规划问题的可行域求作时,要注意不等式表示的区域是相应直线的上方、下方,是否包括边界上的点。利用特殊点进行判断)。B>0,Ax+By+C>0表示直线斜上侧区域;Ax+By+C<0表示直线斜下侧区域;A>0,Ax+By+C>0表示直线斜右侧区域;Ax+By+C<0表示直线斜左侧区域;求最优解注意①目标函数值≠截距②目标函数斜率与区域边界斜率的关系.
已知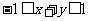 ,
, ,则
,则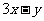 的取值范围是______(答:
的取值范围是______(答: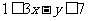 );
);
3、两个不等式相乘时,必须注意同向同正时才能相乘,即同向同正可乘;同时要注意“同号可倒”即
a>b>0,a<b<0。①若ab>0,则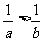 。即不等式两边同号时,不等式两边取倒数,不等号方向要改变。②如果对不等式两边同时乘以一个代数式,要注意它的正负号,如果正负号未定,要注意分类讨论。
。即不等式两边同号时,不等式两边取倒数,不等号方向要改变。②如果对不等式两边同时乘以一个代数式,要注意它的正负号,如果正负号未定,要注意分类讨论。
2、三个二次(一元二次方程,一元二次函数,一元二次不等式)的关系及应用掌握了吗?如何利用二次函数求最值?注意到对二次项系数进行讨论了吗?特别提醒:二次方程 的两个根即为不等式 解集的端点值,也是二次函数 的图像与x轴的交点的横坐标。
1、在求不等式(方程)的解集、定义域及值域时,其结果一定要用集合或区间表示;不能用不等式表示.你会用补集的思想解决有关问题吗?
如:已知关于x的不等式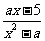 <0的解集为M,若
<0的解集为M,若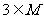 且
且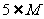 ,求实数a的取值
,求实数a的取值
范围。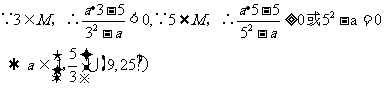
27.[解析]解此题,理解太阳直射点移动与气压带、风带移动关系是首要之处,读准图中所表示的气压带、风带位置所示日期是关键;其次是对相应表述所应该出现的时间要有准确的理解判断。
[答案](1)太阳直射点 北 南(3分)(2)夏至日 春分日或秋分日 冬至日(3分)(3)副热带高气压带 赤道低气压带 (2分)(4)①A;②C;③C;④A。(4分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com