
3.几何性质:
2.标准方程: .
1.定义: .
17、你知道函数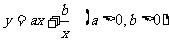 的单调区间吗?(该函数在
的单调区间吗?(该函数在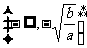 或
或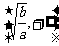 上单调递增;在
上单调递增;在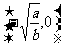 或
或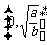 上单调递减)这可是一个应用广泛的函数!其它情况呢?
上单调递减)这可是一个应用广泛的函数!其它情况呢?
16、求值域方法
①配方法:如:求函数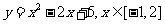 的值域(答:[4,8])
的值域(答:[4,8])
②逆求法(反求法):如: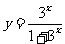 通过反解,用
通过反解,用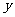 来表示
来表示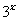 ,再由
,再由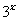 的取值范围,通过解不等式,得出
的取值范围,通过解不等式,得出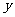 的取值范围(答:(0,1));
的取值范围(答:(0,1));
③换元法:如(1)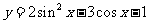 的值域为_____(答:
的值域为_____(答: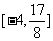 );(2)
);(2)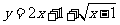 的值域为_____(答:
的值域为_____(答: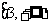 )(令
)(令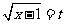 ,
,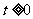 。运用换元法时,要特别要注意新元
。运用换元法时,要特别要注意新元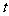 的范围);
的范围);
④三角有界法:转化为只含正弦、余弦的函数,运用三角函数有界性来求。如: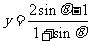 的值域
的值域
⑤不等式法――利用基本不等式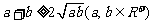 求函数的最值。如设
求函数的最值。如设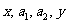 成等差数列,
成等差数列,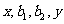 成等比数列,则
成等比数列,则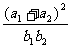 的取值范围是____________.(答:
的取值范围是____________.(答: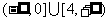 )。
)。
⑥单调性法:函数为单调函数,可根据单调性求值域。如求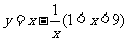 ,
,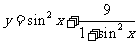 ,
,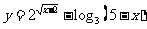 的值域为______(答:
的值域为______(答: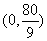 、
、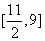 、
、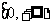 );
);
⑦数形结合:根据函数的几何图形,利用数型结合的方法来求值域。如(1)已知点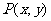 在圆
在圆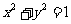 上,求
上,求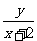 及
及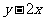 的取值范围(答:
的取值范围(答: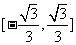 、
、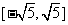 );(2)求函数
);(2)求函数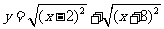 的值域(答:
的值域(答: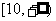 );
);
15、证法:①比较法:差比:作差--变形(分解或通分配方)--定号.另:商比②综合法--由因导果;③分析法--执果索因;④反证法--正难则反。⑤放缩法方法有:
添加或舍去一些项,如: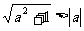 ;
;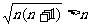
⑥换元法:常用的换元有三角换元和代数换元。如:
已知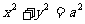 ,可设
,可设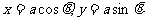 ;
;
⑦最值法,如:a>fmax(x),则a>f(x)恒成立.
14、研究函数问题牢记“定义域优先法”了吗?研究函数问题准备好“数形结合”这个工具了吗?
12、比较大小的常用方法:(1)作差:作差后通过分解因式、配方等手段判断差的符号得出结果;(2)作商(常用于分数指数幂的代数式);(3)分析法;(4)平方法;(5)分子(或分母)有理化;(6)利用函数的单调性;(7)寻找中间量与“0”比,与“1”比或放缩法 ;(8)图象法。其中比较法(作差、作商)是最基本的方法。如(1)设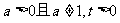 ,比较
,比较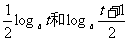 的大小(答:当
的大小(答:当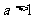 时,
时,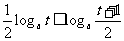 (
(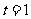 时取等号);当
时取等号);当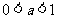 时,
时,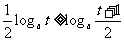 (
(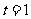 时取等号));(2)设
时取等号));(2)设 ,
,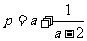 ,
,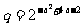 ,试比较
,试比较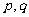 的大小(答:
的大小(答: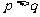 )
)
13、常用不等式:若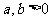 ,(1)
,(1)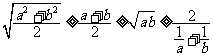 (当且仅当
(当且仅当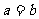 时取等号) ;(2)a、b、c
时取等号) ;(2)a、b、c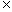 R,
R,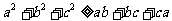 (当且仅当
(当且仅当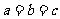 时,取等号);(3)若
时,取等号);(3)若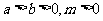 ,则
,则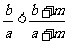 (糖水的浓度问题)。|a|≥a;|a|≥-a
(糖水的浓度问题)。|a|≥a;|a|≥-a
11、实系数一元二次方程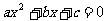 有实数解”转化为“
有实数解”转化为“ ”,你是否注意到必须
”,你是否注意到必须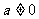 ;当a=0时,“方程有解”不能转化为
;当a=0时,“方程有解”不能转化为 .若原题中没有指出是“二次”方程、函数或不等式,你是否考虑到二次项系数可能为零的情形?例如:
.若原题中没有指出是“二次”方程、函数或不等式,你是否考虑到二次项系数可能为零的情形?例如: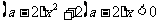 对一切
对一切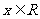 恒成立,求a的取值范围,你讨论了a=2的情况了吗?
恒成立,求a的取值范围,你讨论了a=2的情况了吗?
例:(1)若实数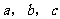 为常数,则“
为常数,则“ 且
且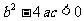 ”是“对任意
”是“对任意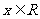 ,有
,有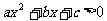 ”的充分不必要条件。(2)关于x的方程2kx2+(8k+1)x+8k=0 有两个不相等的实根,则k的取值范围是 : k>-1/16 且k≠ 0
”的充分不必要条件。(2)关于x的方程2kx2+(8k+1)x+8k=0 有两个不相等的实根,则k的取值范围是 : k>-1/16 且k≠ 0
10、恒成立不等式问题通常解决的方法:借助相应函数的单调性求解,其主要技巧有数形结合法,分离变量法,换元法,最值法;化为一次或二次方程根的分布问题.a≥f(x)恒成立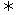 a≥[f(x)]max,;a≤f(x)恒成立
a≥[f(x)]max,;a≤f(x)恒成立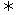 a≤[f(x)]min;
a≤[f(x)]min;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com