
5.(原创题)若一个α角的终边上有一点P(-4,a),且sinα·cosα=,则a的值为________.
解析:依题意可知α角的终边在第三象限,点P(-4,a)在其终边上且sinα·cosα=,易得tanα=或,则a=-4或-.答案:-4或-
4.函数y=++的值域为________.
解析:当x为第一象限角时,sinx>0,cosx>0,tanx>0,y=3;
当x为第二象限角时,sinx>0,cosx<0,tanx<0,y=-1;
当x为第三象限角时,sinx<0,cosx<0,tanx>0,y=-1;
当x为第四象限角时,sinx<0,cosx>0,tanx<0,y=-1.答案:{-1,3}
3.(2008年高考全国卷Ⅱ改编)若sinα<0且tanα>0,则α是第_______象限的角.
答案:三
2.设α为第四象限角,则下列函数值一定是负值的是________.
①tan ②sin ③cos ④cos2α
解析:α为第四象限角,则为第二、四象限角,因此tan<0恒成立,应填①,其余三个符号可正可负.答案:①
1.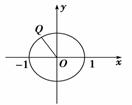 点P从(-1,0)出发,沿单位圆x2+y2=1顺时针方向运动弧长到达Q点,则Q点的坐标为________.
点P从(-1,0)出发,沿单位圆x2+y2=1顺时针方向运动弧长到达Q点,则Q点的坐标为________.
解析:由于点P从(-1,0)出发,顺时针方向运动弧长到达Q点,如图,因此Q点的坐标为(cos,sin),即Q(-,).答案:(-,)
8.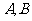 是抛物线
是抛物线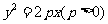 上的两点,且
上的两点,且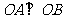 ,
,
(1)求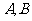 两点的横坐标之积和纵坐标之积;
两点的横坐标之积和纵坐标之积;
(2)求证:直线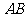 过定点;
过定点;
(3)求弦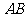 中点
中点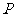 的轨迹方程;
的轨迹方程;
(4)求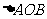 面积的最小值;
面积的最小值;
(5)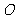 在
在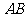 上的射影
上的射影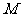 轨迹方程.
轨迹方程.
7.抛物线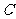 的顶点在坐标原点,对称轴为
的顶点在坐标原点,对称轴为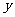 轴,
轴,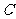 上动点
上动点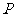 到直线
到直线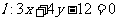 的最短距离为1,求抛物线
的最短距离为1,求抛物线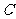 的方程.
的方程.
6.抛物线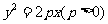 的动弦
的动弦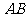 长为
长为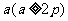 ,则弦
,则弦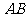 的中点
的中点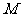 到
到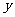 轴的最小距离为
.
轴的最小距离为
.
5.设抛物线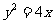 的过焦点的弦的两个端点为A、B,它们的坐标为
的过焦点的弦的两个端点为A、B,它们的坐标为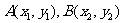 ,若
,若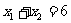 ,那么
,那么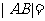 .
.
4.过定点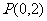 ,作直线
,作直线 与曲线
与曲线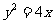 有且仅有1个公共点,则这样的直线
有且仅有1个公共点,则这样的直线 共有
条.
共有
条.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com