
17.上海迪斯尼乐园的具体建设在紧锣密鼓的推进之中,要形成一定规模的主题乐园至少还需要四到五年的时间,其中有三名工人准备参与建设“动物王国”、“魔幻影城”和“梦幻世界”三个主题公园,规划中3个主题公园所含工程项目的个数分别占总工程个数的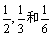 ,现在这3名工人独立从中任选一个项目参与建设.
,现在这3名工人独立从中任选一个项目参与建设.
(1)求他们选择的项目互不相同的概率;
(2)记 为3人中选择的项目属于“魔幻影城”或“梦幻世界”的人数,求
为3人中选择的项目属于“魔幻影城”或“梦幻世界”的人数,求 的分布列及数学期望.
的分布列及数学期望.
16.已知函数f (x) = 2cos2x-2sinxcosx + 1.
(1)设方程f (x) – 1 = 0在(0,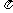 )内的两个零点x1,x2,求x1 + x2的值;
)内的两个零点x1,x2,求x1 + x2的值;
(2)把函数y = f (x)的图象向左平移m (m>0)个单位使所得函数的图象关于点(0,2)对称,求m的最小值.
15.给出以下五个命题:
①若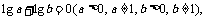 则函数
则函数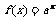 与
与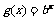 的图象关于x轴对称.
的图象关于x轴对称.
②已知函数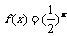 的反函数是y=
的反函数是y= ,则
,则 在
在 上单调递增.
上单调递增.
③为调查参加运动会的1000名运动员的年龄分布情况,从中抽查了100名运动员的档案进行调查,个体是被抽取的每个运动员;
④用独立性检验(2×2列联表)来考察两个变量是否具有相关关系时,计算出的随机变量K2的观测值越大,则说明“X与Y有关系的可能性越大” .
其中正确命题的序号是 .
14.某同学高三阶段12次数学考试的成绩呈现前几次与后几次均连续上升,中间几次连续下降的趋势;现有三种函数模型。①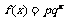 ,②
,②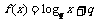 ,
,
③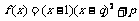 (其中p,q为正常数,且q>2).较准确反映数学成绩与考试序次关系,应选 作为模拟函数;若
(其中p,q为正常数,且q>2).较准确反映数学成绩与考试序次关系,应选 作为模拟函数;若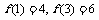 ,求出所选函数
,求出所选函数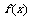 的解析式
.
的解析式
.
13.设函数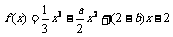 有两个极值
有两个极值 点,其中一个在区间(0,1)内,另一个在区间(1,2)内,则
点,其中一个在区间(0,1)内,另一个在区间(1,2)内,则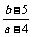 的取值范围是 .
的取值范围是 .
12.公比为4的等比数列{bn}中,若Tn是数列{bn}的前n项积,则有 仍成等比数列,且公比为4100;类比上述结论,在公差为3的等差数列{an}中,若Sn是{an}的前n项和,则有____
仍成等比数列,且公比为4100;类比上述结论,在公差为3的等差数列{an}中,若Sn是{an}的前n项和,则有____
_________________________也成等差数列,该等差数列的公差为 .
11.已知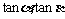 是方程
是方程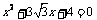 的两根,
的两根,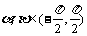 ,则
,则 .
.
10.从8名女生,4名男生中选出6名学生组成课外小组,如果按性别分层抽样,则不同的抽取方法种数为 .
9.已知复数z满足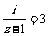 (i为参数单位),则复数z的实部与虚部之和为
.
(i为参数单位),则复数z的实部与虚部之和为
.
8.已知函数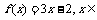 R.规定:给定一个实数x0,赋值
R.规定:给定一个实数x0,赋值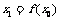 ,若
,若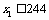 ,则继续赋值
,则继续赋值 以此类推,若
以此类推,若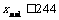 ,则
,则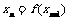 ,否则停止赋值,如果得到xn称为赋值了n次(n∈N*).已知赋值k次后该过程停止,则x0的取值范围是 ( )
,否则停止赋值,如果得到xn称为赋值了n次(n∈N*).已知赋值k次后该过程停止,则x0的取值范围是 ( )
A.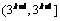 B.
B.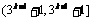
C.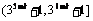 D.
D.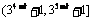
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com