
21. 几何证明选讲
AB是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线交AB延长线于C,若DA=DC,求证AB=2BC
22(本小题满分10分)选修4-4:坐标系与参数方程
已知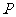 为半圆
为半圆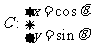 (
( 为参数,
为参数,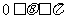 )上的点,点
)上的点,点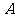 的坐标为
的坐标为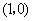 ,
,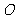 为坐标原点,点
为坐标原点,点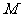 在射线
在射线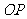 上,线段
上,线段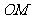 与
与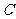 的弧
的弧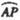 的长度均为
的长度均为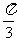 。
。
(Ⅰ)以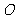 为极点,
为极点,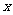 轴的正半轴为极轴建立极坐标系,求点
轴的正半轴为极轴建立极坐标系,求点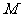 的坐标;
的坐标;
(Ⅱ)求直线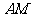 的参数方程
的参数方程
23(本小题满分10分)选修4-5:不等式选讲
已知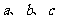 均为正数,证明:
均为正数,证明: ,并确定
,并确定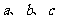 为何值时,等号成立。
为何值时,等号成立。
20.(本小题满分12分)
设函数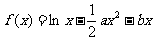 .
.
(Ⅰ)当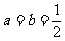 时,求
时,求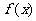 的最大值;
的最大值;
(Ⅱ)令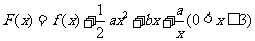 ,以其图象上任意一点
,以其图象上任意一点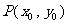 为切点的切线的斜率
为切点的切线的斜率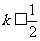 恒成立,求实数
恒成立,求实数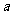 的取值范围;
的取值范围;
(Ⅲ)当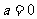 ,
,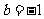 时,方程
时,方程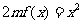 有唯一实数解,求正数
有唯一实数解,求正数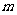 的值
的值
 (从以下三个题中任选一个作答)
(从以下三个题中任选一个作答)
19. (本小题满分12分)
(本小题满分12分)
已知点A(-1,0)、B(1,0)和动点M满足: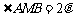 ,且
,且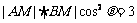 ,动点M的轨迹为曲线C,过点B的直线交C于P、Q两点.
(1)求曲线C的方程;
(2)求△APQ面积的最大值.
,动点M的轨迹为曲线C,过点B的直线交C于P、Q两点.
(1)求曲线C的方程;
(2)求△APQ面积的最大值.
18.(本小题满分12分)
已知各项都不相等的等差数列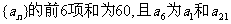 的等比中项。
的等比中项。
(I)求数列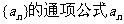 ;
;
(II)若数列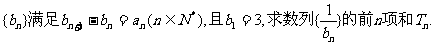
17.(本小题满分12分)
 如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.
16.(本小题满分12分)
先后随机投掷2枚正方体骰子,其中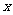 表示第
表示第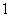 枚骰子出现的点数,
枚骰子出现的点数,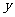 表示第
表示第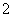 枚骰子出现的点数.
枚骰子出现的点数.
(Ⅰ)求点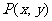 在直线
在直线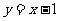 上的概率;
上的概率;
(Ⅱ)求点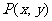 满足
满足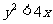 的概率.
的概率.
15.(本小题满分12分)
已知向量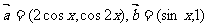
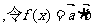 .
.
(Ⅰ) 求 f (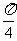 )的值;(Ⅱ)求
)的值;(Ⅱ)求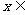
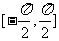 时,f (x)的单调递增区间.
时,f (x)的单调递增区间.
14.已知函数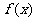 的导函数为
的导函数为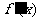 ,且满足
,且满足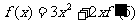 ,
,
则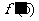 = .
= .
13.已知实数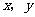 满足
满足 ,则
,则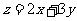 的最小值是
.
的最小值是
.
12.某大型超市销售的乳类商品有四种:纯奶、酸奶、婴幼儿奶粉、成人奶粉,且纯奶、酸奶、婴幼儿奶粉、成人奶粉分别有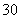 种、
种、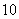 种、
种、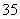 种、
种、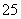 种不同的品牌.现采用分层抽样的方法从中抽取一个容量为
种不同的品牌.现采用分层抽样的方法从中抽取一个容量为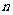 的样本进行三聚氰胺安全检测,若抽取的婴幼儿奶粉的品牌数是
的样本进行三聚氰胺安全检测,若抽取的婴幼儿奶粉的品牌数是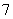 ,则
,则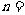 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com