
(1) B (2)C (3)B (4) C (5)C
(6) B (7) D (8)D (9)B (10) C
(18)(本小题14分)在△ABC中,a, b, c 分别是角A ,B ,C 的对边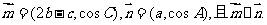
(i)求角A的大小;
(ii)记 B=x ,作出函数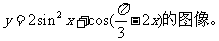
(19)(本小题14分)设数列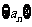 满足条件:
满足条件: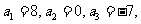 且数列
且数列
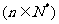 是等差数列。
是等差数列。
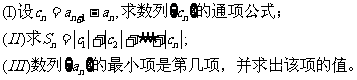
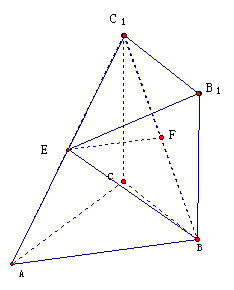
(20)(本题满分14分)如图,矩形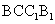 所在平面垂直于三角形ABC所在平面,且
所在平面垂直于三角形ABC所在平面,且
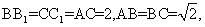 又E\F分别是
又E\F分别是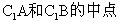 。
。

(21)(本题15分)已知函数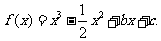

(22)(本题15分)已知直线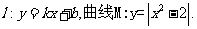

2010年杭州市第二次高考科目教学质量检测
数学文科卷评分标准
(11)若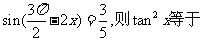 ______
______
(12)依次写出数列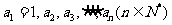 的法则如下:如果
的法则如下:如果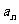 为自然数,则写
为自然数,则写
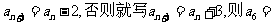 ______(注意0是自然数)
______(注意0是自然数)
(13)已知A,B
是圆O: 上两点,且
上两点,且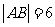 ,若以AB为直径的圆M恰好经过点C(1,-1),则圆心M的轨迹方程是_______.
,若以AB为直径的圆M恰好经过点C(1,-1),则圆心M的轨迹方程是_______.
(14)观察下列等式:

可以推测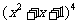 展开式中,系数最大项是_______.
展开式中,系数最大项是_______.
(15)从1至8这八个自然数中,任取两个不同的数,这两个数的和是3的倍数的概率是___
(16)如果实数x,y满足条件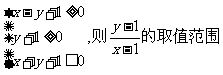 ______
______
(17)已知函数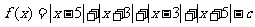 ,若存在正常数m, 使f(m)=0,则不等式f(x)<f(m)的解集是______
,若存在正常数m, 使f(m)=0,则不等式f(x)<f(m)的解集是______
(1)
设集合A=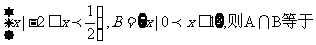 ( )
( )
A. 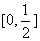 B.
B. 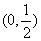 C.
C. 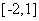 D.
D. 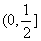
(2)在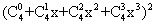 的展开式中,所有项的系数和为( )
的展开式中,所有项的系数和为( )
A.64 B.224 C. 225 D.256
(3)使“lgm<1”成立的一个充分不必要条件是( )
A.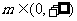 B.
B.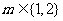 C.
C. 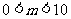 D.m<1
D.m<1
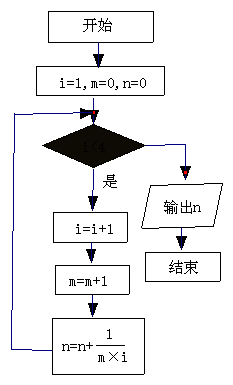 (4)如图,是一个几何体的三视图,侧视图与正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的侧面积为( )
(4)如图,是一个几何体的三视图,侧视图与正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的侧面积为( )
A. 6 B. 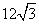 C.24 D.3
C.24 D.3

(5)如图,是一个算法的程序框图,该算法输出的结果是( )
A. 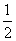 B.
B. 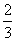 C.
C. 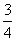 D.
D. 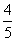
(6)平面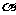 的斜线L与平面
的斜线L与平面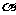 所成的角是45°,则L与平面
所成的角是45°,则L与平面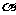 内所有不过斜足的直线所成的角中,最大的角是( )
内所有不过斜足的直线所成的角中,最大的角是( )
A.45° B.90° C.135° D.60°
(7)已知向量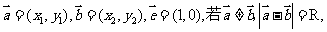
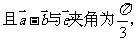
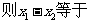 ( )
( )
A. R B. 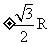 C.
C. 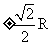 D.
D. 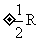
(8)过双曲线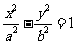 (a>0,b>0)的一个焦点F引它的渐近线的垂线,垂足为M,延长FM交y轴于E,若FM=ME, 则该双曲线的离心率为( )
(a>0,b>0)的一个焦点F引它的渐近线的垂线,垂足为M,延长FM交y轴于E,若FM=ME, 则该双曲线的离心率为( )
A. 3
B. 2 C. 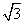 D.
D.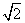
(9)设函数f(x)=ln(x-1)(2-x)的定义域是A,函数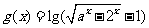 的定义域是B,若
的定义域是B,若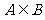 ,则正数a的取值范围( )
,则正数a的取值范围( )
A. a>3 B. 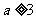 C.
C.  D.
D. 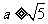
(10)如图,阴影是集合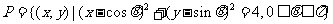 在平面直角坐标系上表示的点集,则阴影中间形如“水滴”部分的面积等于( )
在平面直角坐标系上表示的点集,则阴影中间形如“水滴”部分的面积等于( )
A.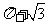 B.
B. 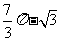 C.
C. 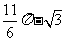 D.
D. 

21. (本小题满分12分)
解:(1)f (x)定义域为{x |
x<1},f ′(x) = 2ax 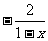
假设存在实数a,使f (x)在x =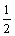 处取极值,则
处取极值,则
f ′(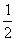 ) = a –
4 = 0, ∴a = 4
------------------ 3分
) = a –
4 = 0, ∴a = 4
------------------ 3分
此时,f ′(x) = 8x  =
=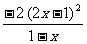
当x <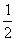 时,f ′(x) < 0;当
时,f ′(x) < 0;当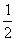 <x<1时,f ′(x) < 0.
<x<1时,f ′(x) < 0.
∴x =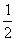 不是f (x)的极值点,
不是f (x)的极值点,
故不存在实数a,使f (x)在x =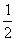 处极值
------------- 6分
处极值
------------- 6分
(2)解法一:依题意知:当x∈[-1,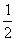 ]时,f ′(x) ≤0恒成立,
]时,f ′(x) ≤0恒成立,
f ′(x)≤0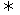 2ax –
2ax – 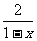 ≤0
≤0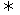 ax≤
ax≤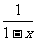
①当x = 0时,不等式显然成立;
②当-1≤x<0时,a≥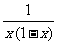
∵-1≤x<0 ∴ x (1 – x) = – (x –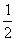 )2 +
)2 + 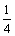 ∈
∈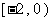
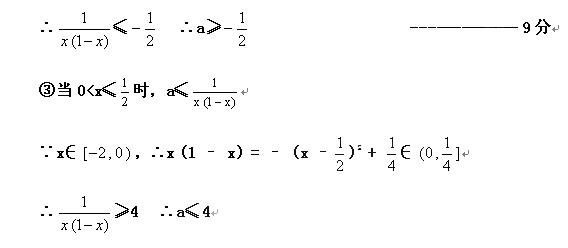 综上可知,
综上可知,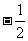 ≤a≤4为所求
---------------- 12分
≤a≤4为所求
---------------- 12分
解法二:依题意知:当x∈[-1,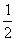 ]时,f ′(x) ≤0恒成立,
]时,f ′(x) ≤0恒成立,
f ′(x) ≤0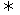 2ax –
2ax – 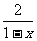 ≤0
≤0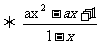 ≥0
≥0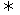 ax2 – ax
+ 1≥0
ax2 – ax
+ 1≥0
令g (x) = ax2 – ax + 1 = a (x )2 + 1
)2 + 1 , x∈
, x∈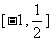
①当a = 0时,g (x) = 1>0成立;
②当a>0时,g (x)在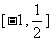 上递减,则
上递减,则
g (x)min = g (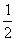 ) = 1
) = 1 ≥0 ∴0<a≤4
------------ 9分
≥0 ∴0<a≤4
------------ 9分
③当a<0时,g (x)在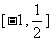 上递增,则
上递增,则
g (x)min = g (-1) = 2a
+ 1≥0 ∴0>a≥
综上, ≤a≤4为所求
-------------------- 12分
≤a≤4为所求
-------------------- 12分
[命题分析]本题主要考查运用导数研究函数性质的方法,分类讨论的数学思想和分析推理能力.
 [解](1)
[解](1)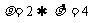 ,所以
,所以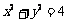 ;因为
;因为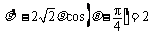 ,
,
所以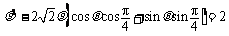 ,所以
,所以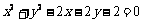 ---5分
---5分
(2)将两圆的直角坐标方程相减,得经过两圆交点的直线方程为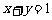 .化为极坐标方程为
.化为极坐标方程为 ,即
,即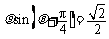 . ---10分
. ---10分
20. (本小题满分12分)
解:(1)设该工人在2006年一年里所得奖金为X,则X是一个离散型随机变量.由于该工人每季度完成任务与否是等可能的,所以他每季度完成任务的概率等于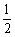 ,所以,
,所以,
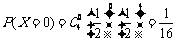 ,
,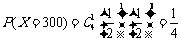 ,
,
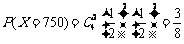 ,
,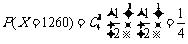 ,
,
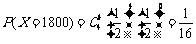 .
-------------------------------------8分
.
-------------------------------------8分
 其分布列为
其分布列为
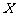 |
0 |
300 |
750 |
1260 |
1800 |

19. (本小题满分12分)
(本小题满分12分)
解:(Ⅰ)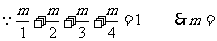
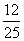 ---------------
4分
---------------
4分
(Ⅱ)
|
X |
1 |
2 |
3 |
4 |
|
P |
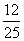 |
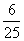 |
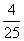 |
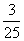 |
---- 8分
(Ⅲ)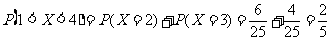 ----------12分
----------12分
18. (本小题满分12分)
解:(1)当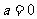 时,
时,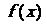 在
在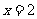 处不能取得极值,∵
处不能取得极值,∵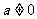 .--------2分
.--------2分
当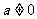 时,
时,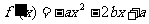 ,∴
,∴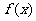 在
在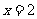 处取得极值,且
处取得极值,且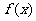 在
在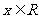 上均可导,故
上均可导,故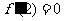 ,即:
,即: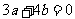 . -------5分
. -------5分
∴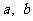 应满足:
应满足: 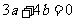 且
且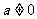 -------6分
-------6分
(2)由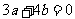 得
得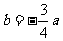 ,∴
,∴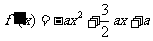 .
.
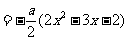
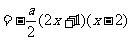 -------8分
-------8分
17.(本小题满分12分)
解:(1)a=20 --------------4分
(2)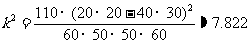 -------------------------8分
-------------------------8分
因为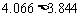 ,所以有99%的把握,认为数学成绩与物理成绩有关,判断出错的概率只有1%.
--------------------------------------------12分
,所以有99%的把握,认为数学成绩与物理成绩有关,判断出错的概率只有1%.
--------------------------------------------12分
13.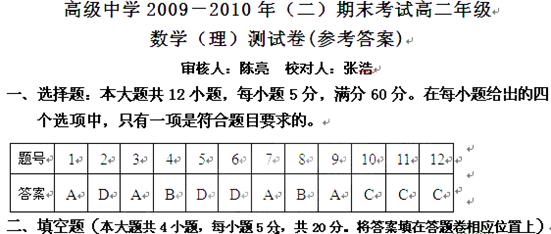 (1.5,4) 14. 45 ;74 15.
(1.5,4) 14. 45 ;74 15.
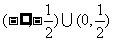 16.②④
16.②④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com