6、在分类讨论时,分类要做到“不重不漏、层次分明，最后要进行总结．

5、解答题中，如果要应用教材中没有的重要结论，那么在解题过程中要给出简单的证明。

4、解答多参型问题时，关键在于恰当地引出参变量,　想方设法摆脱参变量的困绕．这当中，参变量的分离、集中、消去、代换以及反客为主等策略，是解答这类问题的通性通法)

3、解答开放型问题时，需要思维广阔全面，知识纵横联系．

2、解答应用型问题时，最基本要求是什么？(审题、找准题目中的关键词，设未知数、列出函数关系式、代入初始条件、注明单位、答)解应用题:审题(理顺数量关系)、建模、求模、验证.

在填写填空题中的应用题的答案时, 在做应用题时,不要忘了单位． 运算后的单位要弄准，不要忘了“答”及变量的取值范围。

1、解答填空题时应注意什么？(特殊化，图解，等价变形)要审准题、结果要简明要符合要求。如：从小到大、从大到小排列，错误(正确)命题是‥‥‥还有单位等。

11、你会利用圆锥曲线的定义解题吗?你注意到定义中的关键词了吗?(例如椭圆中定长大于定点之间的距离等).解析几何中的基本方法:联立方程组,消元,判别式,韦达定理,弦长公式等.

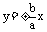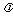10、解题注意:①考虑圆锥曲线焦点位置,抛物线还应注意开口方向,以避免错误②求圆锥曲线方程常用待定系数法、定义法、轨迹法③焦点、准线有关问题常用圆锥曲线定义来简化运算或证明过程④运用假设技巧以简化计算.如:中心在原点,坐标轴为对称轴的椭圆(双曲线)方程可设为Ax²+Bx²＝1;共渐进线的双曲线标准方程可设为为参数,≠0);抛物线y²=2px上点可设为(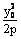,y₀);直线的另一种假设为x=my+a;⑤解焦点三角形常用正余弦定理及圆锥曲线定义.

9、轨迹方程求法:直接法(建系、设点、列式、化简、定范围)、定义法、几何法、代入法(动点P(x,y)依赖于动点Q(x₁,y₁)而变化,Q(x₁,y₁)在已知曲线上,用x、y表示x₁、y₁,再将x₁、y₁代入已知曲线即得所求方程)、参数法、交轨法等.

8、相交弦问题①用直线和圆锥曲线方程消元得二次方程后,注意用判别式、韦达定理、弦长公式；注意二次项系数为0的讨论；注意对参数分类讨论和数形结合、设而不求思想的运用；注意焦点弦可用焦半径公式,其它用弦长公式，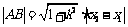

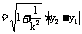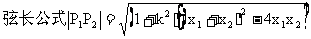
涉及弦中点与斜率问题常用“点差法”