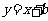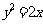1．直线与抛物线，当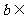　 时，有且只有一个公共点；当　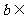 时，有两个不同的公共点；当　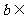　 时，无公共点．

2．弦的中点或中点弦的问题，除利用韦达定理外，也可以运用“差分法”(也叫“点差法”)．

1．直线与圆锥曲线的位置关系的判定方法：

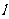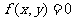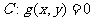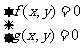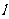直线：和曲线的公共点坐标是方程组的解，和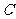的公共点的个数等于方程组不同解的个数．这样就将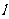和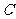的交点问题转化为方程组的解问题研究，对于消元后的一元二次方程，必须讨论二次项系数和判别式，若能数形结合，借助图形的几何性质则较为简便．

2．会利用直线与圆锥曲线的方程所组成的方程组消去一个变量，将交点问题问题转化为一元二次方程根的问题，结合根与系数关系及判别式解决问题．

1．掌握直线与圆锥曲线的位置关系的判定方法，能够把研究直线与圆锥曲线的位置关系的问题转化为研究方程组的解的问题；

11、保持良好的心态，是正常发挥、高考取胜的关键！

要真正梳理清楚这些知识，关键是在理解的基础上去记忆，决不能死记硬背。同学们有了清晰的知识背景，和完善的知识结构的同时，再进行必要的独立练习，巩固“双基”，就能提高综合解题能力和数学应试水平。

在这里我也要提醒同学们，在数学复习中要避免两个极端，要么，埋头看书、整理，懒得独立练习；要么，埋头练习、陷入题海。前者，忽视了数学是一门思维的科学，离开了解题实践，数学思维无法展开，无法将学到的知识、方法内化为自己的能力。后者，忽视了有的放矢，容易重复机械操练，缺乏反思、提炼，事倍功半。

此外,同学们在梳理知识和独立练习的过程中，要勤于反思，举一反三，多联系知识的发生和形成过程，多总结通性通法和规范思路，多关注思想方法和探究创新，在复习中抱着开放的心态和锲而不舍的精神，开展“研究性复习”，始终保持旺盛的斗志和灵活的思维，数学成绩一定能够取得比较大的突破。

10、由于高考采取电脑阅卷，所以一定要努力使字迹工整，卷面整洁，切记在规定区域答题。

9、高考数学试题主要从以下几个方面对数学思想方法进行考查：

①　 常用数学方法：配方法、换元法、待定系数法、数学归纳法、参数法、消元法等；

②　 数学逻辑方法：分析法、综合法、反证法、归纳法、演绎法等；

③　 数学思维方法：观察与分析、概括与抽象、分析与综合、特殊与一般、类比、归纳和演绎等；

④　 常用数学思想：函数与方程思想、数形结合思想、分类讨论思想、转化(化归)思想等。

8、解答信息型问题时，透彻理解问题中的新信息，这是准确解题的前提．

7、解答选择题的特殊方法是什么？(顺推法，估算法，特例法，特征分析法，直观选择法，逆推验证法等)