
18.(本题满分12分)
解:(Ⅰ)连接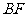 ,不妨设
,不妨设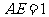 ,则
,则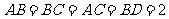 ,于是
,于是
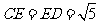 ,
,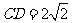 ,所以
,所以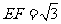 ,
,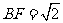 ,
,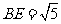 …………… 3分
…………… 3分
所以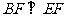 ,又
,又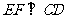 ,又
,又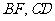 为两条相交直线
为两条相交直线
故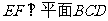 ……………………………………6分
……………………………………6分
(Ⅱ)由(Ⅰ)可知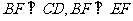 ,所以
,所以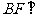 面
面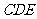
又过作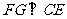 ,交
,交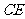 于点
于点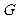 ,连接
,连接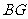
因此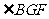 为二面角
为二面角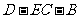 的平面角
……………………9分
的平面角
……………………9分
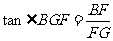 ,而
,而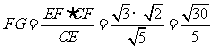
所以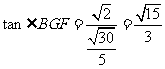 ………………………………12分
………………………………12分
17.(本题满分12分)
解:(Ⅰ)因为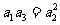 ,所以
,所以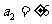 …………………………2分
…………………………2分
又因为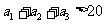 ,所以
,所以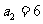 ,故公比
,故公比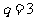 …………4分
…………4分
所以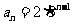 ………………………6分
………………………6分
(Ⅱ)设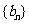 公差为
公差为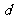 ,所以
,所以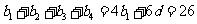 …………………8分
…………………8分
由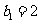 ,可知
,可知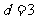 ,
,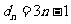 ……………………10分
……………………10分
所以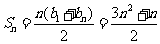 ……………………
……………………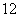 分
分
13. 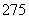 14.
14.
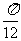 15.
15. 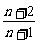 16.
16. 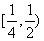
24.(本小题满分10分)选修4-5:不等式选讲
若关于的不等式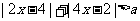 恒成立,求的取值范围.
恒成立,求的取值范围.
2010年四校联考第二次高考模拟考试
数学试卷(理工类)评分标准
23.(本小题满分10分)选修4-4:坐标系与参数方程
已知直线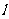 的极坐标方程为
的极坐标方程为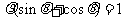 ,曲线
,曲线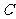 的参数方程为
的参数方程为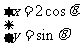 (
(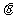 为参数).
为参数).
(Ⅰ)求直线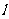 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线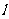 与曲线
与曲线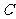 交于,四两点,原点为
交于,四两点,原点为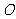 ,求
,求 的面积.
的面积.
22.(本小题满分10分)选修4-1:几何证明选讲
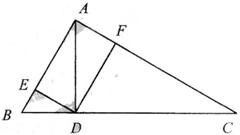 已知
已知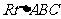 中,
中,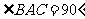 ,
,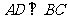 ,
,
垂足为,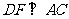 ,垂足为,
,垂足为,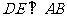 ,
,
垂足为.
求证:(Ⅰ)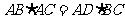 ;
;
(Ⅱ)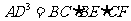
21.(本小题满分12分)
已知点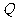 是抛物线
是抛物线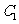 :
: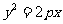 (
(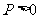 )上异于坐标原点
)上异于坐标原点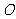 的点,过点
的点,过点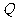 与抛物线
与抛物线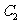 :
: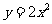 相切的两条直线分别交抛物线
相切的两条直线分别交抛物线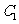 于点A,B.
于点A,B.
(Ⅰ)若点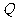 的坐标为
的坐标为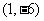 ,求直线
,求直线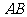 的方程及弦
的方程及弦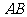 的长;
的长;
(Ⅱ)判断直线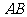 与抛物线
与抛物线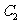 的位置关系,并说明理由.
的位置关系,并说明理由.
20.(本小题满分12分)
已知定义在正实数集上的函数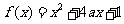 ,
,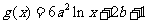 ,其中
,其中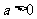 .
.
(Ⅰ)设两曲线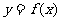 ,
,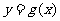 有公共点,且在该点处的切线相同,用表示
有公共点,且在该点处的切线相同,用表示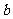 ,并求
,并求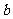 的最大值;
的最大值;
(Ⅱ)设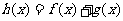 ,证明:若
,证明:若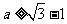 ,则对任意
,则对任意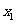 ,
,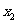
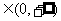 ,
,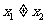 有
有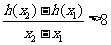 .
.
19.(本小题满分12分)
由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:

(Ⅰ)指出这组数据的众数和中位数;
(Ⅱ)若视力测试结果不低丁5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(Ⅲ)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记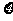 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求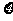 的分布列及数学期望.
的分布列及数学期望.
18.(本小题满分12分)
已知在多面体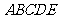 中,
中,
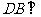 平面
平面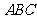 ,
,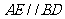 ,
,
且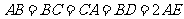 ,
,
为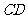 的中点,
的中点,
(Ⅰ)求证: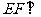 平面
平面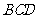 ;
;
(Ⅱ)求二面角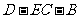 的正切值.
的正切值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com