
21.(本小题满分14分)
设数列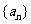 满足
满足 令
令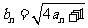
(I)
试证明数列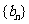 是等差数列
是等差数列 ,并求数列
,并求数列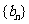 的通项公式;
的通项公式;
(II)
令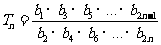 ,是否存在实数
,是否存在实数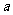 ,使得不等式
,使得不等式 对一切
对一切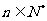 都成立?若存在,求出
都成立?若存在,求出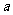 的取值
的取值
范围;若不存在,请说明理由。




20.(本小题满分13分)
已知椭圆C的中心在原点,焦点在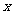 轴上,它的一个顶点B的坐标为(0,1),离心率等于
轴上,它的一个顶点B的坐标为(0,1),离心率等于 。斜率为1的直线
。斜率为1的直线 与椭
与椭 圆C交于M,N两点。
圆C交于M,N两点。
(I) 求椭圆C的方程;
(II)
问椭圆C的右焦点F是否可以为 的重心?若可以
的重心?若可以 ,求出直线
,求出直线 的方程;若不可以,请
的方程;若不可以,请 说
说 明理由。
明理由。
19.(本小题满分12分)
设函数
(I)
若对任意的 ,不等式
,不等式 都成立,求实数
都成立,求实数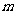 的最小值;
的最小值;
(II)
求函数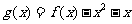 在区间
在区间 上的极值。
上的极值。
18.(本小题满分12分)
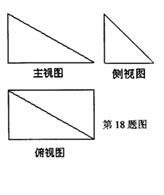
已知四棱锥P-ABCD的三视图如右图。该棱锥中,
PA=AB=1,PD与平面ABCD所成角是30°,点
F是PB的中点,点E在棱BC上移动。
(I)画出该棱锥的直观图并证明:无论点E在棱
BC的何处,总有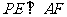 ;
;
(II)连接DE,设G为DE上一动点,当三棱锥
P-AGE的体积为 时,试确定G在DE上的位置。
时,试确定G在DE上的位置。
17.(本小题满分12分)
某市教育部门为了解高三学生素质测评情况,对其中的2000名学生的测评结果进行了统计,其中优秀、良好、合格三个等级的男、女学生人数如下表(其中x,y分 别表示优秀等级的男、女学生人数)
别表示优秀等级的男、女学生人数)
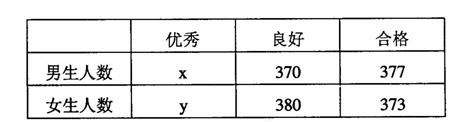
(I)
若用分层抽样法在这2000份综合素质测评结果中随机抽取60份进行比较分析,应抽 取综合素质测评结果是优秀等级的多少份?
取综合素质测评结果是优秀等级的多少份?
(II)
若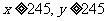 ,求优秀等级的学生中女生人数比男生人数多的概率。
,求优秀等级的学生中女生人数比男生人数多的概率。
16.(本小题满分12分)
已知向量 ,向量
,向量 ,函数
,函数 。
。
(I)
求函数 的最小正周期;
的最小正周期;
(II)
求函数 的单调递增区间;
的单调递增区间;
(III)
求函数 在区间
在区间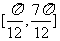 上的值域。
上的值域。
15.设奇函数 在
在 上是增函数,若
上是增函数,若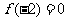 ,则不等式
,则不等式 的解集是
的解集是
。
14.给出下列四个结论:
①命题 的否定是
的否定是
②“若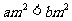 ,则
,则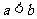 ”的逆命题为真;
”的逆命题为真;
③已知直线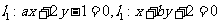 ,则
,则 的充要条件是
的充要条件是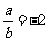 ;
;
④对于任意实数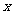 ,有
,有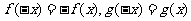 且
且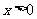 时,
时, ,
, ,则
,则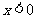 时,
时,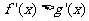 。
。
其中正确结论的序号是 (填上所有正确结论的序号)
13.已知P是直线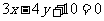 上的动点,PA、PB是圆
上的动点,PA、PB是圆 的两条切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值为 。
的两条切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值为 。
12.某校从高一年级期末考 试学生中抽出60名学生
试学生中抽出60名学生
的数学成绩,将其(均为整数)分成六组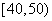 ,
, 画出部分频率分布直方图如上,由此估计期末考似高一年级数学的平均分为
。
画出部分频率分布直方图如上,由此估计期末考似高一年级数学的平均分为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com