
22.He’s _______ to fail the exam if he doesn’t do any revision.
A.bound B.fit 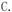 about D.easy
about D.easy
第一节 单项填空(共15小题;每小题1分,满分15分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
21.- So she told you you’d got the job?
- ________, but she said they were impressed with me.
A.Not really B.Not particularly
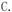 Not exactly D.Not specially
Not exactly D.Not specially
(17)(本小题满分10分)
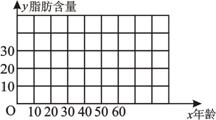
在关于人体脂肪含量 (百分比)和年龄
(百分比)和年龄 关系的研究中,得到如下一组数据
关系的研究中,得到如下一组数据
年 龄 |
23 |
27 |
39 |
41 |
45 |
50 |
脂肪含量 |
9.5 |
17.8 |
21.2 |
25.9 |
27.5 |
28.2 |
(Ⅰ)画出散点图,判断 与
与 是否具有相关关系;
是否具有相关关系;
 (Ⅱ)通过计算可知
(Ⅱ)通过计算可知 ,
,
请写出 对
对 的回归直线方程,并计算
的回归直线方程,并计算
出 岁和
岁和 岁的随机误差.
岁的随机误差.
(18)(本小题满分12分)
已知二次函数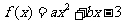 在
在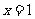 处取得极值,且在
处取得极值,且在 点处的切线与直线
点处的切线与直线 平行.
平行.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)求函数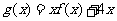 的单调递增区间.
的单调递增区间.
(19)(本小题满分12分)
已知函数 .
.
(Ⅰ)讨论函数 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(Ⅱ)若函数 在
在 上为增函数,求
上为增函数,求 的取值范围.
的取值范围.
(20)(本小题满分12分)
为迎接上海世博会某旅游部门开发了一种新产品,每件产品的成本是15元,,销售价是20元,月平均销售 件.通过改进工艺,产品的成本不变,质量和技术含量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含量提高,市场分析的结果表明,如果产品的销售价提高的百分率为 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是 (元).
(元).
(Ⅰ)写出 关于
关于 的函数关系式;
的函数关系式;
(Ⅱ)改进工艺后,确定该纪念品的售价,使得旅游部门销售该纪念品的月平均利润最大.
(21)(本小题满分12分)
设数列 的前
的前 项和为
项和为 ,且满足
,且满足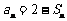
 .
.
(Ⅰ)求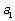 ,
, ,
, ,
, 的值并写出其通项公式;
的值并写出其通项公式;
(Ⅱ)用三段论证明数列 是等比数列.
是等比数列.
(22)(本小题满分12分)
已知函数 是
是 上的增函数,
上的增函数, ,b∈R.
,b∈R.
(Ⅰ)若 ,求证:
,求证: ;
;
(Ⅱ)判断(Ⅰ)中命题的逆命题是否成立,并证明你的结论.
|

|
版权所有:()
2009-2010学年度第二学期期末考试
(13)已知 ,且
,且 ,则
,则
(14)在工程技术中,常用到双曲正弦函数 和双曲余弦函数
和双曲余弦函数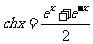 ,它们与我们学习过的正、余弦函数有相似之处,如:对于余弦数有cos(x+y)=cosxcosy-sinxsiny,而关于双曲余弦函数有ch(x+y)=chxchy+shxshy.请你类比此公式,写出关于双曲余弦函数的一个新公式______________________.
,它们与我们学习过的正、余弦函数有相似之处,如:对于余弦数有cos(x+y)=cosxcosy-sinxsiny,而关于双曲余弦函数有ch(x+y)=chxchy+shxshy.请你类比此公式,写出关于双曲余弦函数的一个新公式______________________.
(15)函数 与
与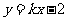 有相同的零点, 则实数
有相同的零点, 则实数 的值为_________.
的值为_________.
(16)已知 ,则适合方程
,则适合方程 的x值为__________.
的x值为__________.
(1)若集合 ,
, ,则集合
,则集合 等于
等于
(A) (B)
(B)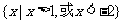
(C) (D)
(D)
 (2)在复平面内,复数
(2)在复平面内,复数 对应的点位于
对应的点位于
(A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限
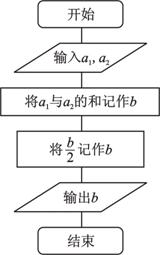
(3)图中所示的是一个算法的流程图.已知 ,输出
,输出
的结果为 ,则
,则 的值为
的值为
(A)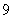
(B)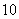
(C)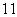
(D)
(4)函数 的定义域是
的定义域是
(A) (B)
(B)
(C) (D)
(D)
(5)抛物线 在点
在点 处的切线方程是
处的切线方程是
(A)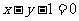 (B)
(B)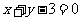
(C) (D)
(D)
(6)下面几种推理过程是演绎推理的是
(A)某校高三有8个班,1班有51人,2班有53人,3班有52人,由此推测各班人数都超过50人;
(B)由三角形的性质,推测空间四面体的性质;
(C)平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分;
(D)在数列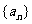 中,
中, ,由此归纳出
,由此归纳出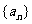 的通项公式.
的通项公式.
(7)在线性回归模型 中,下列说法正确的是
中,下列说法正确的是
(A) 是一次函数
是一次函数
(B)因变量 是由自变量
是由自变量 唯一确定的
唯一确定的
(C)随机误差 是由于计算不准确造成的,可以通过精确计算避免随机误差e的产生
是由于计算不准确造成的,可以通过精确计算避免随机误差e的产生
(D)因变量 除了受自变量
除了受自变量 的影响外,可能还受到其它因素的影响,这些因素会导致随机误差
的影响外,可能还受到其它因素的影响,这些因素会导致随机误差 的产生
的产生
(8)设函数 ,且
,且 ,则
,则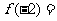
(A)2 (B)-2 (C)1 (D)-1
(9)若函数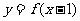 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线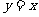 对称,则
对称,则 等于
等于
(A) (B)
(B) (C)
(C)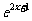 (D)
(D)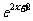
(10)用反证法证明命题:“若直线AB、CD是异面直线,则直线AC、BD也是异面直线”的过程归纳为以下三个步骤:
①则A,B,C,D四点共面, 所以AB、CD共面,这与AB、CD是异面直线矛盾;
②所以假设错误, 即直线AC、BD也是异面直线;
③假设直线AC、BD是共面直线;
则正确的序号顺序为
(A)①→②→③ (B)③→①→②
(C)①→③→② (D)②→③→①
(11)已知函数 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时, ,那么当
,那么当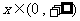 时,
时, =
=
(A)  (B)
(B) 
(C)  (D)
(D) 
(12)在研究某新措施对“甲流”的防治效果问题时,得到如下列联表:
|
|
存活数 |
死亡数 |
合 计 |
|
新措施 |
132 |
18 |
150 |
|
对照 |
114 |
36 |
150 |
|
合计 |
246 |
54 |
300 |
由表中数据可得 ,故我们由此认为“新措施对防治甲流有效”的把握为(A)0 (B)
,故我们由此认为“新措施对防治甲流有效”的把握为(A)0 (B) (C)
(C) (D)
(D)
第Ⅱ卷 (非选择题,共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com