4.

图4－4－5

为纪念伽利略将望远镜用于天文观测400周年，2009年被定为以“探索我的宇宙”为主题的国际天文年．我国发射的“嫦娥一号”卫星经过一年多的绕月运行，完成了既定任务，于2009年3月1日16时13分成功撞月．如图4－4－5为“嫦娥一号”卫星撞月的模拟图，卫星在控制点①开始进入撞月轨道．假设卫星绕月球做圆周运动的轨道半径为R，周期为T，引力常量为G.根据题中信息，以下说法正确的是(　)

A．可以求出月球表面的重力加速度

B．可以求出月球对“嫦娥一号”卫星的引力

C．“嫦娥一号”卫星在控制点①处应减速

D．“嫦娥一号”在地面的发射速度大于11.2 km/s

解析：根据G＝m₂R，已知卫星的T、R和引力常量G，可以求月球的质量m₁；因为不知道“嫦娥一号”卫星的质量，故无法知道月球对“嫦娥一号”卫星的引力，B项错误；在控制点①，卫星要做向心运动，故需要减速，C项正确；11.2 km/s是第二宇宙速度，是卫星脱离地球引力的束缚成为太阳的人造行星的最小发射速度，而“嫦娥一号”卫星并不能脱离地球引力的范围，故其发射速度小于11.2 km/s，D项错误．

答案：C

3．质量相等的甲、乙两颗卫星分别贴近某星球表面和地球表面围绕其做匀速圆周运动，已知该星球和地球的密度相同，半径分别为R和r，则(　)

A．甲、乙两颗卫星的加速度之比等于R∶r　

B．甲、乙两颗卫星所受的向心力之比等于1∶1

C．甲、乙两颗卫星的线速度之比等于1∶1　

D．甲、乙两颗卫星的周期之比等于R∶r

解析：由F＝G和M＝ρπR³可得万有引力F＝GπRmρ，又由牛顿第二定律F＝ma可得，A正确．卫星绕星球表面做匀速圆周运动时，万有引力等于向心力，因此B错误．由F＝GπRmρ，F＝m可得，选项C错误．由F＝GπRmρ，F＝mR可知，周期之比为1∶1，故D错误．

答案：A

2．(2009·全国Ⅰ，19)天文学家新发现了太阳系外的一颗行星．这颗行星的体积是地球的4.7倍，质量是地球的25倍．已知某一近地卫星绕地球运动的周期约为1.4小时，引力常量G＝6.67×10^－11 N·m²/kg²，由此估算该行星的平均密度约为(　)　

A．1.8×10³ kg/m³　 　　B．5.6×10³ kg/m³ 　　C．1.1×10⁴ kg/m³　 　D．2.9×10⁴ kg/m³

解析：近地卫星绕地球做圆周运动时，所受万有引力充当其做圆周运动的向心力，即：G＝m²R，由密度、质量和体积关系M＝ρ·πR³解两式得：ρ＝≈5.60×10³ kg/m³.由已知条件可知该行星密度是地球密度的25/4.7倍，即ρ＝5.60×10³× kg/m³＝2.9×10⁴ kg/m³.

答案：D

1.

图4－4－4

三颗人造地球卫星A、B、C在同一平面内沿不同的轨道绕地球做匀速圆周运动，且绕行方向相同，已知R_A＜R_B＜R_C.若在某一时刻，它们正好运行到同一条直线上，如图4－4－4所示．那么再经过卫星A的四分之一周期时，卫星A、B、C的位置可能是(　)

答案：C

5.

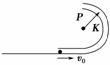
图4－3－10

(2010·诸城模拟)如图4－3－10所示，半径为R，内径很小的光滑半圆管道竖直放置，质量为m的小球以某一速度进入管内，小球通过最高点P时，对管壁的压力为0.5mg.求：

(1)小球从管口飞出时的速率；

(2)小球落地点到P点的水平距离．

解析：(1)分两种情况，当小球对管下部有压力时，则有mg－0.5mg＝，v₁＝.当小球对管上部有压力时，则有mg+0.5mg＝，v₂＝

(2)小球从管口飞出做平抛运动，2R＝gt²，t＝2 ，x₁＝v₁t＝R，x₂＝v₂t＝R.

答案：(1) 或 　(2)R或R

4.

图4－3－9

某实验中学的学习小组在进行科学探测时，一位同学利用绳索顺利跨越了一道山涧，他先用绳索做了一个单摆(秋千)，通过摆动，使自身获得足够速度后再平抛到山涧对面，如图4－3－9所示，若他的质量是M，所用绳长为L，在摆到最低点B处时的速度为v，离地高度为h，当地重力加速度为g，则：

(1)他用的绳子能承受的最大拉力不小于多少？

(2)这道山涧的宽度不超过多大？

解析：(1)该同学在B处，由牛顿第二定律得：F－Mg＝M，

解得：F＝Mg+M，即他用的绳子能承受的最大拉力不小于Mg+M.

(2)对该同学做平抛运动的过程由运动学公式得：水平方向有：x＝vt，竖直方向有：　 h＝gt²，

解得：x＝v ，即这道山涧的宽度不超过v .

答案：(1)Mg+M　(2)v

3.

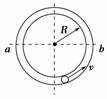
图4－3－8

(2010·西南师大附中模拟)如图4－3－8所示，小球在竖直放置的光滑圆形管道内做圆周运动，内侧壁半径为R，小球半径为r，则下列说法正确的是(　)

A．小球通过最高点时的最小速度v_min＝

B．小球通过最高点时的最小速度v_min＝0

C．小球在水平线ab以下的管道中运动时，内侧管壁对小球一定无作用力

D．小球在水平线ab以上的管道中运动时，外侧管壁对小球一定有作用力

解析：小球沿管上升到最高点的速度可以为零，故A错误，B正确；小球在水平线ab以下的管道中运动时，由外侧管壁对小球的作用力F_N与球重力在背离圆心方向的分力F_mg的合力提供向心力，即：F_N－F_mg＝m，因此，外侧管壁一定对球有作用力，而内侧壁无作用力，C正确；小球在水平线ab以上的管道中运动时，小球受管壁的作用力与小球速度大小有关，D错误．

答案：BC

2.

图4－3－7

m为在水平传送带上被传送的小物体(可视为质点)，A为终端皮带轮，如图4－3－7所示，已知皮带轮半径为 r，传送带与皮带轮间不会打滑，当m可被水平抛出时，A轮每秒的转数最少是(　)

A. 　 　　 　　B. 　 　 　　C.　 　D.

解析：当m被水平抛出时只受重力的作用，支持力N＝0.在圆周最高点，重力提供向心力，即mg＝，所以v＝.而v＝2πf·r，所以f＝＝ ，所以每秒的转数最小为 ，A正确．

答案：A

1.

图4－3－6

质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点，如图4－3－6所示，当轻杆绕轴BC以角速度ω匀速转动时，小球在水平面内做匀速圆周运动，绳a在竖直方向，绳b在水平方向，当小球运动到图示位置时，绳b被烧断的同时杆子停止转动，则(　)

A．小球仍在水平面内做匀速圆周运动

B．在绳被烧断瞬间，a绳中张力突然增大

C．若角速度ω较小，小球在垂直于平面ABC的竖直平面内摆动

D．若角速度ω较大，小球可在垂直于平面ABC的竖直平面内做圆周运动

解析：绳b烧断前，竖直方向合力为零，即F_a＝mg，烧断b后，因惯性，要在竖直面内做圆周运动，且F_a′－mg＝m，所以F_a′＞F_a，A错B对，当ω足够小时，小球不能摆过AB所在高度，C对，当ω足够大时，小球在竖直面内能通过AB上方最高点，从而做圆周运动，D对．

答案：BCD

12．

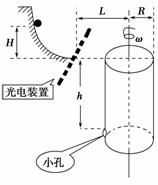
图4－2－26

如图4－2－26所示，小球从光滑的圆弧轨道下滑至水平轨道末端时，光电装置被触动，控制电路会使转筒立刻以某一角速度匀速连续转动起来．转筒的底面半径为R，已知轨道末端与转筒上部相平，与转筒的转轴距离为L，且与转筒侧壁上的小孔的高度差为h；开始时转筒静止，且小孔正对着轨道方向．现让一小球从圆弧轨道上的某处无初速滑下，若正好能钻入转筒的小孔(小孔比小球略大，小球视为质点，不计空气阻力，重力加速度为g)，求：

(1)小球从圆弧轨道上释放时的高度为H；

(2)转筒转动的角速度ω.

解析：(1)设小球离开轨道进入小孔的时间为t，则由平抛运动规律得h＝gt²，

L－R＝v₀t

小球在轨道上运动过程中机械能守恒，故有mgH＝mv

联立解得：t＝ ，H＝.

(2)在小球做平抛运动的时间内，圆筒必须恰好转整数转，小球才能钻进小孔，

即ωt＝2nπ(n＝1,2,3…)．所以ω＝nπ (n＝1,2,3…)

答案：(1)　(2)nπ (n＝1,2,3…)