
5.设数列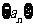 的前
的前 项和为
项和为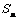 ,点
,点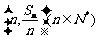 均在函数
均在函数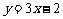 的图象上.
的图象上.
则数列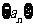 的通项公式为
.
的通项公式为
.
4. 已知x>0,y>0,x,a,b,y成等差数列,x,c,d,y成等比数列,则的最小值是________.高
3.已知函数 ,则不等式
,则不等式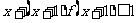 的解集是( )
的解集是( )
A.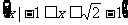 B.
B. 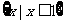
C. 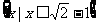 D.
D.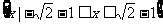
2. 等差数列{an}和{bn}的前n项和分别用Sn和Tn表示,若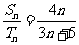 ,则
,则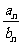 的值为( )
的值为( )
A  B
B 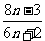 C
C 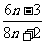 D
D 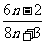
1.公差不为零的等差数列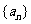 的前
的前 项和为
项和为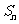 .若
.若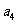 是
是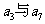 的等比中项,
的等比中项, 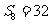 ,则
,则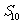 等于 ( )
等于 ( )
A. 18 B. 24 C. 60 D. 90
5.数列与概率的综合
数列与概率的综合考查,虽然不是经常但很有新意,这种命题也体现了在知识交汇处命题的指导思想.
例9.将一骰子连续抛掷三次,它落地时向上的点数依次成等差数列的概率为( )
A.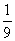 B.
B. C.
C.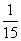 D.
D.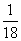
解析:一骰子连续抛掷三次得到的数列共有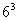 个,其中为等差数列有三类:
个,其中为等差数列有三类:
(1)公差为0的有6个;(2)公差为1或-1的有8个;(3)公差为2或-2的有4个,共有18个,成等差数列的概率为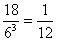 ,选B.
,选B.
点评:本题是以数列和概率的背景出现,题型新颖而别开生面,有采取分类讨论,分类时要做到不遗漏,不重复.
[思想方法]
[例1]已知等比数列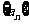 的首项为
的首项为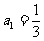 ,公比
,公比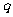 满足
满足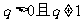 .又已知
.又已知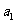 ,
,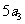 ,
,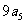 成等差数列.
(1)求数列
成等差数列.
(1)求数列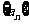 的通项.
的通项.
(2)令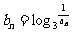 ,求证:对于任意
,求证:对于任意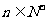 ,都有
,都有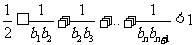
解析:(1)∵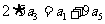 ∴
∴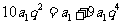 ∴
∴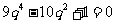
∵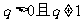 ∴
∴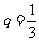 ∴
∴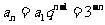
(2)证明:∵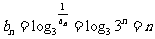 ,
, 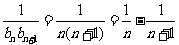
∴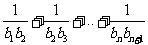

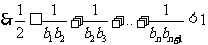 .
.
[分析]转化思想是数学中的重要思想,把复杂的问题转化成清晰的问题是我们解题的指导思想.本题中的第(2)问,采用裂项相消法,将式子进行转化后就可以抵消很多项,从而只剩下首末两项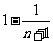 ,进而由n的范围证出不等式.
,进而由n的范围证出不等式.
[例2]在数列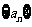 中,
中,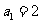 ,
,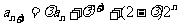
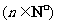 ,其中
,其中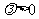 .
.
(Ⅰ)求数列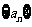 的通项公式;
的通项公式;
(Ⅱ)求数列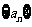 的前
的前 项和
项和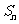 ;
;
(Ⅲ)证明存在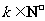 ,使得
,使得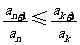 对任意
对任意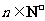 均成立.
均成立.
解析:(Ⅰ)  ,
,
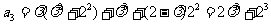 ,
,
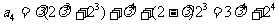 .
.
由此可猜想出数列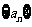 的通项公式为
的通项公式为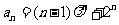 .
.
以下用数学归纳法证明.
(1)当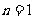 时,
时,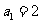 ,等式成立.
,等式成立.
(2)假设当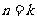 时等式成立,即
时等式成立,即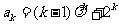 ,
,
那么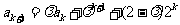
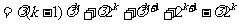
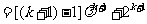 .
.
这就是说,当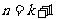 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式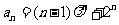 对任何
对任何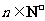 都成立.
都成立.
(Ⅱ)解:设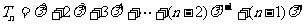 , ①
, ①
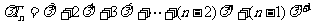 ②
②
当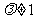 时,①式减去②式,
时,①式减去②式,
得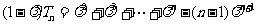
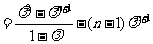 ,
,
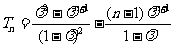
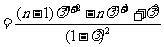 .
.
这时数列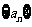 的前
的前 项和
项和 .
.
当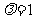 时,
时,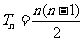 .这时数列
.这时数列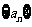 的前
的前 项和
项和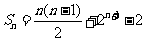 .
.
(Ⅲ)证明:通过分析,推测数列 的第一项
的第一项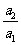 最大,下面证明:
最大,下面证明:
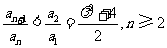 . ③
. ③
由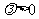 知
知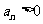 ,要使③式成立,只要
,要使③式成立,只要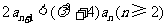 ,
,
因为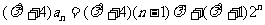
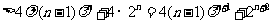
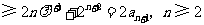 .
.
所以③式成立.
因此,存在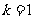 ,使得
,使得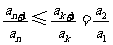 对任意
对任意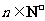 均成立.
均成立.
[分析]分类讨论思想是数学中的重要思想,本题以数列的递推关系式为载体,综合考查了等比数列的前 项和公式、数列求和、不等式的证明等基础知识与基本方法,第2问体现了对运用分类讨论的考查.
项和公式、数列求和、不等式的证明等基础知识与基本方法,第2问体现了对运用分类讨论的考查.
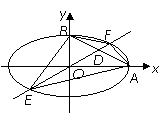 [例3]设椭圆中心在坐标原点,A(2,0)、B(0,1)是它的两个顶点,直线
[例3]设椭圆中心在坐标原点,A(2,0)、B(0,1)是它的两个顶点,直线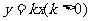 与AB相交于点D,与椭圆相较于E、F两点.
与AB相交于点D,与椭圆相较于E、F两点.
(Ⅰ)若 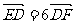 ,求k的值;
,求k的值;
(Ⅱ)求四边形AEBF面积的最大值.
解析:(Ⅰ)依题设得椭圆的方程为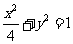 ,
,
直线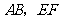 的方程分别为
的方程分别为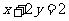 ,
,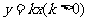 .
.
如图,设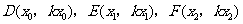 ,其中
,其中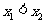 ,
,
且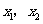 满足方程
满足方程 ,
,
故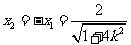 .①
.①
由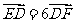 知
知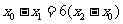 ,得
,得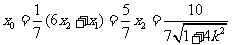 ;
;
由 在
在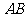 上知
上知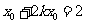 ,得
,得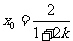 .
.
所以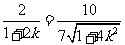 ,
,
化简得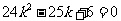 ,
,
解得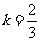 或
或 .
.
(Ⅱ)解法一:根据点到直线的距离公式和①式知,点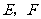 到
到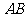 的距离分别为
的距离分别为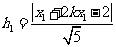
 ,
,
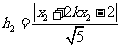
 .
.
又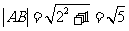 ,所以四边形
,所以四边形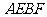 的面积为
的面积为
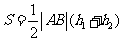
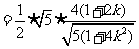
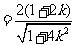
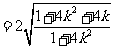
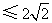 ,
,
当 ,即当
,即当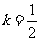 时,上式取等号.所以
时,上式取等号.所以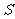 的最大值为
的最大值为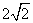 .
.
解法二:由题设,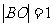 ,
,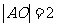 .
.
设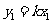 ,
,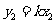 ,由①得
,由①得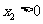 ,
,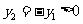 ,
,
故四边形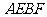 的面积为
的面积为
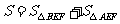

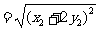
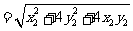
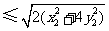
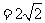 ,
,
当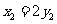 时,上式取等号.所以
时,上式取等号.所以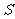 的最大值为
的最大值为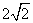 .
.
[分析]方程与函数思想是数学中的重要思想,该题对于k的求解就是通过建立k的方程,然后解出的;而对于四边形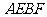 的面积的求解,是通过构造面积
的面积的求解,是通过构造面积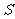 关于k的函数关系,然后根据均值不等式来解决其最值问题.
关于k的函数关系,然后根据均值不等式来解决其最值问题.
[专题演练]
4.数列与不等式、简易逻辑等的综合
数列是培养推理论证能力的极好载体,将数列的知识与推理证明的方法交织在一起进行考查,是新课程高考中的一个亮点,常常荣归纳、猜想、数学归纳法、分类讨论、等价转化等数学思想和方法于一体,对能力的要求较高.
例7.设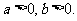 若
若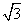 是
是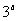 与
与 的等比中项,则
的等比中项,则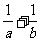 的最小值为( )
的最小值为( )
A.8
B.4
C.1
D.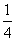
答案:B
解析:因为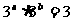 ,所以
,所以 ,
,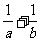

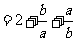
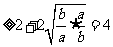 ,当且仅当
,当且仅当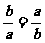 即
即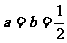 时“=”成立,故选择B.
时“=”成立,故选择B.
点评:本小题考查指数式和对数式的互化,以及均值不等式求最值的运用,考查了变通能力.
例8.设数列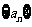 满足
满足 为实数.
为实数.
(Ⅰ)证明: 对任意
对任意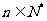 成立的充分必要条件是
成立的充分必要条件是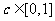 ;
;
(Ⅱ)设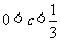 ,证明:
,证明: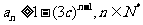 ;
;
(Ⅲ)设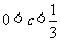 ,证明:
,证明: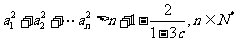 .
.
解析: (1) 必要性: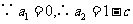 ,又
,又 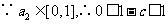 ,即
,即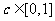 .
.
充分性 :设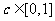 ,对
,对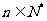 用数学归纳法证明
用数学归纳法证明 ,
,
当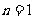 时,
时,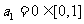 .假设
.假设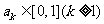 ,
,
则 ,且
,且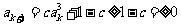 ,
,
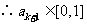 ,由数学归纳法知
,由数学归纳法知 对所有
对所有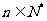 成立.
成立.
(2) 设 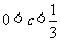 ,当
,当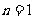 时,
时,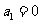 ,结论成立.
,结论成立.
当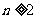 时,
时,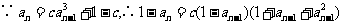 ,
,
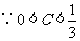 ,由(1)知
,由(1)知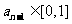 ,所以
,所以 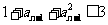 且
且  ,
,
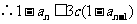 ,
,
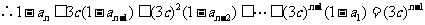 ,
,
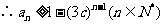 .
.
(3) 设 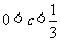 ,当
,当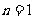 时,
时, ,结论成立,
,结论成立,
当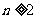 时,由(2)知
时,由(2)知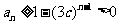 ,
,
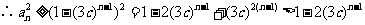 ,
,
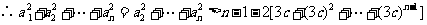
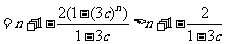 .
.
点评:该题综合考查了等比数列的求和、不等式的性质的应用、充分必要条件和数学归纳法等,具有较高的难度,对逻辑推理能力的考查要求较高.
3.函数与数列的综合
高考试题中经常将函数与数列综合在一起,设计综合性较强的解答题,考查数列的概念、性质、通项及求和公式等主干知识和分析问题、解决问题的逻辑推理能力.
例6.知函数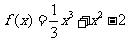 .
.
(Ⅰ)设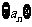 是正数组成的数列,前n项和为
是正数组成的数列,前n项和为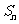 ,其中
,其中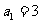 .若点
.若点 (n∈N*)在函数
(n∈N*)在函数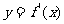 的图象上,求证:点
的图象上,求证:点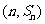 也在
也在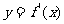 的图象上;
的图象上;
(Ⅱ)求函数 在区间
在区间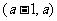 内的极值.
内的极值.
解析:(Ⅰ)证明:
因为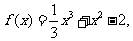 所以
所以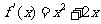 ,
,
由点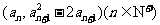 在函数
在函数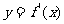 的图象上,
的图象上,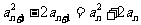
 ,
又
,
又 ,
,
所以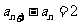 ,
,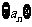 是
是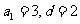 的等差数列,
的等差数列,
所以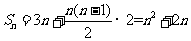 ,又因为
,又因为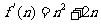 ,所以
,所以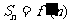 ,
,
故点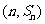 也在函数
也在函数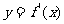 的图象上.
的图象上.
(Ⅱ)解: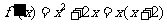 ,令
,令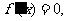 得
得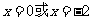 .
.
当x变化时,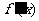 ﹑
﹑ 的变化情况如下表:
的变化情况如下表:
|
x |
(-∞,-2) |
-2 |
(-2,0) |
|
f(x) |
+ |
0 |
- |
|
f(x) |
↗ |
极大值 |
↘ |
注意到 ,从而
,从而
①当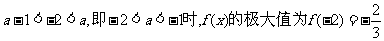 ,此时
,此时 无极小值;
无极小值;
②当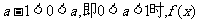 的极小值为
的极小值为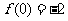 ,此时
,此时 无极大值;
无极大值;
③当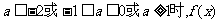 既无极大值又无极小值.
既无极大值又无极小值.
点评:本小题主要考查函数极值、等差数列等基本知识,考查分类与整合、转化与化归等数学思想方法,考查分析问题和解决问题的能力.
2.函数与不等式综合
不等式与函数有着密切的联系,其中线性规划求目标函数的最值是近几年高考的热点问题之一,经常以选择题或填空题出现.有不少关于最值方面的问题,通常用二次函数的配方法求最值或用均值不等式求最值,考题经常以与不等式有关的实际应用问题出现.在应用不等式解决实际问题时,要注意以下四点:
①理解题意,设变量.设变量时一般把要求最值的变量定为自变量;
②建立相应的函数关系式,把实际问题抽象为函数的最值问题;
③在定义域内,求出函数的最值;
④正确写出答案.
 例3.设x,y满足约束条件
例3.设x,y满足约束条件 ,若目标函数z=ax+by(a>0,b>0)的值是最大值为12,则
,若目标函数z=ax+by(a>0,b>0)的值是最大值为12,则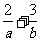 的最小值为(
)
的最小值为(
)
A.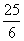 B.
B.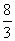 C.
C.
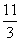 D. 4
D. 4
答案:A
解析:不等式表示的平面区域如图所示阴影部分,当直线ax+by= z(a>0,b>0)过直线x-y+2=0与直线3x-y-6=0的交点(4,6)时,目标函数z=ax+by(a>0,b>0)取得最大12,即4a+6b=12,即2a+3b=6, 而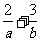 =
=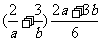
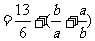
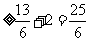 ,故选A.
,故选A.
点评:本题综合地考查了线性规划问题和由基本不等式求函数的最值问题.要求能准确地画出不等式表示的平面区域,并且能够求得目标函数的最值,对于形如已知2a+3b=6,求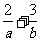 的
的
最小值常用乘积进而用基本不等式解答.
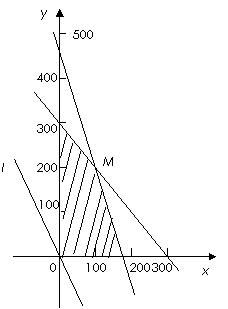
例4.本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为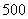 元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是
万元.
元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是
万元.
答案:70
 解析:设公司在甲电视台和乙电视台做广告的时间分别为
解析:设公司在甲电视台和乙电视台做广告的时间分别为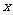 分钟和
分钟和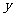 分钟,总收益为
分钟,总收益为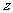 元,由题意得
元,由题意得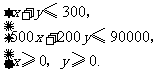
目标函数为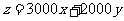 .
.
二元一次不等式组等价于
作出二元一次不等式组所表示的平面区域,即可行域.
如图:作直线 ,即
,即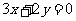 .
.
平移直线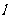 ,从图中可知,当直线
,从图中可知,当直线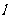 过
过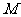 点时,目标函数取得最大值.
点时,目标函数取得最大值.
联立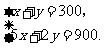 解得
解得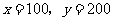 .
.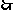 点
点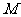 的坐标为
的坐标为 .
.
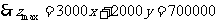 (元).
(元).
点评:本题是线性规划的实际应用问题,需要通过审题理解题意,找出各量之间的关系,找出线性约束条件,写出所研究的目标函数,通过数形结合解答问题.用线性规划的方法解决实际问题能提高学生分析问题、解决问题的能力,随着课改的深入,这类试题应该是高考的热点题型之一.
例5.设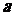 为实数,函数
为实数,函数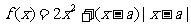 .
.
(1)若 ,求
,求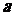 的取值范围;
的取值范围;
(2)求 的最小值;
的最小值;
(3)设函数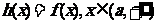 ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式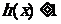 的解集.
的解集.
解析:(1)若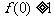 ,则
,则 ;
;
(2)当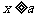 时,
时,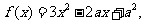
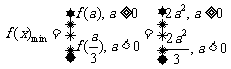 ,
,
当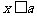 时,
时,
 ,
,
综上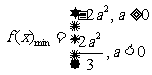 ;
;
(3)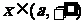 时,
时,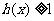 得
得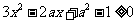 ,
,
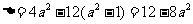
当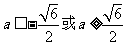 时,
时,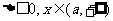 ;
;
当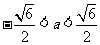 时,△>0,得:
时,△>0,得: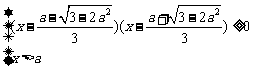 ;
;
讨论得:当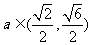 时,解集为
时,解集为 ;
;
当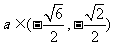 时,解集为
时,解集为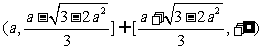 ;
;
当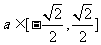 时,解集为
时,解集为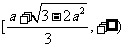 .
.
点评:本小题主要考查函数的概念、性质、图象及解一元二次不等式等基础知识,考查灵活运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力.
1.等差数列与等比数列的综合
等差数列与等比数列都是高考命题的重点知识,考题经常将它们综合在一起综合考查等差数列和等比数列的概念、性质、通项公式、求和公式等基础知识和基本性质的灵活应用,对基本的运算要求比较高.
例1.设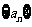 是公差不为0的等差数列,
是公差不为0的等差数列,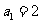 且
且 成等比数列,则
成等比数列,则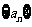 的前
的前 项和
项和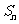 =( )
=( )
A. B.
B.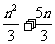 C.
C.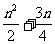 D.
D.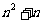
答案:A
解析:设数列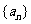 的公差为
的公差为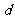 ,则根据题意得
,则根据题意得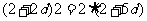 ,解得
,解得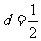 或
或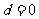 (舍去),所以数列
(舍去),所以数列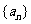 的前
的前 项和
项和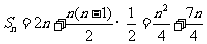 .
.
例2.等比数列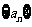 的前n项和为
的前n项和为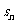 ,且4
,且4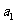 ,2
,2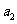 ,
,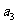 成等差数列.若
成等差数列.若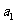 =1,则
=1,则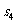 =( )
=( )
(A)7 (B)8 (3)15 (4)16
解析: 4
4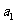 ,2
,2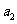 ,
,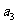 成等差数列,
成等差数列,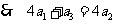 ,即
,即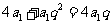 ,
,
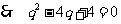 ,
,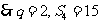 ,因此选C.
,因此选C.
点评:该类题目综合考查了等差数列和等比数列的概念、通项公式和等比数列的求和公式等,基础性较强,综合程度较小,要求具有较熟练的运算能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com