
11.下列离子方程式正确的是
A.在稀氨水中通入过量CO2:2NH3·H2O+CO2=2 NH4++CO32-
B.Na2SO3溶液使酸性KMnO4溶液褪色:5SO32- + 6H+ + 2MnO4- == 5SO42- + 2Mn2+ 3H2O
C.用银氨溶液检验乙醛中的醛基:
CH3CHO
+2Ag(NH3)2OH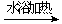 CH3COO- + NH4+
+3NH3 + 2Ag↓+ H2O
CH3COO- + NH4+
+3NH3 + 2Ag↓+ H2O
D.往苯酚钠溶液通入少量CO2:CO2 + H2O + 2C6H5O- 2C6H5OH
+ 2CO32-
2C6H5OH
+ 2CO32-
10. 某探究小组利用丙酮的溴代反应(CH3COCH3+Br2---→CH3COCH2Br+HBr)来研究反应物浓度与反应速率的关系。反应速率
某探究小组利用丙酮的溴代反应(CH3COCH3+Br2---→CH3COCH2Br+HBr)来研究反应物浓度与反应速率的关系。反应速率 通过测定溴的颜色消失所需的时间来确定。在一定温度下,获得如下实验数据:
通过测定溴的颜色消失所需的时间来确定。在一定温度下,获得如下实验数据:
|
实验 序号 |
初始浓度 c/mol·L-1 |
溴颜色消失所需时间 t/s |
||
|
CH3COCH3 |
HCl |
Br2 |
||
|
① |
0.80 |
0.20 |
0.0010 |
290 |
|
② |
1.60 |
0.20 |
0.0010 |
145 |
|
③ |
0.80 |
0.40 |
0.0010 |
145 |
|
④ |
0.80 |
0.20 |
0.0020 |
580 |
 分析实验数据所得出的结论不正确的是
分析实验数据所得出的结论不正确的是
 A. 增大c(CH3COCH3),v(Br2)增大 B. 实验②和③的v(Br2)相等
A. 增大c(CH3COCH3),v(Br2)增大 B. 实验②和③的v(Br2)相等
 C. 增大c(HCl),v(Br2)增大
D. 增大c(Br2),v(Br2)增大
C. 增大c(HCl),v(Br2)增大
D. 增大c(Br2),v(Br2)增大
9.设阿伏加德罗常数(NA)的数值为nA,下列说法正确的是
A.标准状况下,11.2L以任意比例混合的氮气和氧气所含的原子数为nA B.一定条件下,0.1mol铁与0.1mol Cl2充分反应,转移的电子数约为0.3 nA C.常温常压下,1 mol氦气含有的核外电子数为4 nA
D.标准状况下,nA个NO分子和0.5nA个O2分子混合后气体的总体积为33.6 L
|
8.下列说法正确的是
A.SiH4比CH4稳定 B.O2-半径比F-的小
C.Na和Cs属于第ⅠA族元素,Cs失电子能力比Na的强
D.P和As属于第ⅤA族元素,H3PO4酸性比H3AsO4的弱
7.下列叙述或实验不符合绿色化学理念的是( )
A.用废动植物油脂经反应改性制“生物柴油”,代替柴油作内燃机燃料
B.采用银作催化剂,用乙烯和氧气制取环氧乙烷(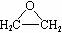 )
)
C.在萃取操作的演示实验中,将CCl4萃取溴水改为CCl4萃取碘水
D.用铜和稀HNO3反应制取Cu(NO3)2
9.(10年广州市中考六模)如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
(1) 求直线AB的解析式;
(2) 当t为何值时,△APQ与△AOB相似?
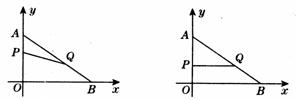 (3) 当t为何值时,△APQ的面积为
(3) 当t为何值时,△APQ的面积为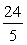 个平方单位?
个平方单位?
答案:
(1)
设直线AB的解析式为y=kx+b
由题意,得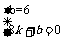 解得
解得
所以,直线AB的解析式为y=-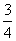 x+6.
x+6.
(2)由AO=6, BO=8 得AB=10
所以AP=t ,AQ=10-2t
1) 当∠APQ=∠AOB时,△APQ∽△AOB.
所以 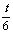 =
= 解得 t=
解得 t=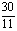 (秒)
(秒)
2) 当∠AQP=∠AOB时,△AQP∽△AOB.
所以 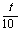 =
=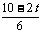 解得 t=
解得 t=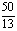 (秒)
(秒)
(3)过点Q作QE垂直AO于点E.
在Rt△AOB中,Sin∠BAO=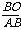 =
=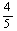
在Rt△AEQ中,QE=AQ·Sin∠BAO=(10-2t)·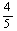 =8 -
=8 -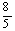 t 2分S△APQ=
t 2分S△APQ=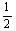 AP·QE=
AP·QE=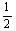 t·(8-
t·(8-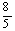 t)
t)
=-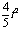 +4t=
+4t=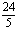 解得t=2(秒)或t=3(秒).
解得t=2(秒)或t=3(秒).
8.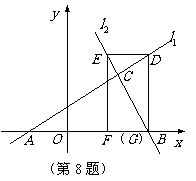 (2010浙江永嘉)如图,已知
(2010浙江永嘉)如图,已知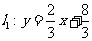 直线与直线
直线与直线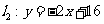 相交于点C,
相交于点C,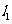 、
、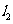 分别交
分别交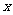 轴于A、B两点.矩形DEFG的顶点D、E分别在直线
轴于A、B两点.矩形DEFG的顶点D、E分别在直线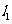 、
、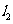 上,顶点
上,顶点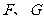 都在
都在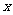 轴上,且点
轴上,且点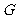 与点
与点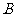 重合.
重合.
(1)求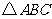 的面积;
的面积;
(2)求矩形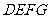 的边
的边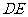 与
与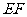 的长;
的长;
(3)若矩形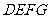 从点B出发,沿
从点B出发,沿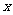 轴以每秒1个单位长度的速度向点A平移,设移动时间为
轴以每秒1个单位长度的速度向点A平移,设移动时间为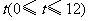 秒,矩形
秒,矩形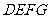 与
与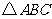 重叠部分的面积为
重叠部分的面积为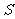 ,求
,求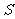 关于
关于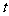 的函数关系式,并写出相应的
的函数关系式,并写出相应的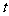 的取值范围.
的取值范围.
(1)解:∵A(-4,0) B(8,0) C(5,6)
∴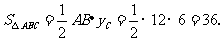
|
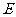
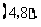
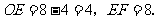
(3)解: 当
当 时,如图1,矩形
时,如图1,矩形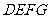 与
与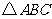 重叠部分为五边形
重叠部分为五边形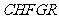
(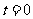 时,为四边形
时,为四边形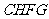 ).过
).过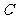 作
作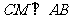 于
于 ,则
,则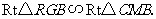

∴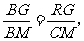 即
即 ∴
∴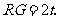
AF=8-t
∴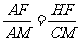
即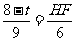
∴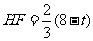
∴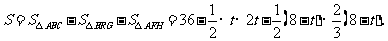
|
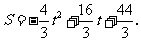
②当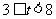 时,如图2,矩形DEFG与△ABC重叠部分为梯形QFGR(t=8时,为△ARG),则AF=8-t , AG=12-t 由Rt△AFQ∽Rt△AGR∽Rt△AMC得
时,如图2,矩形DEFG与△ABC重叠部分为梯形QFGR(t=8时,为△ARG),则AF=8-t , AG=12-t 由Rt△AFQ∽Rt△AGR∽Rt△AMC得
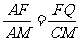 ,
,
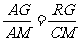 即
即  ,
,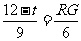
∴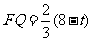 ,
, 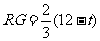
∴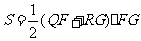 =
=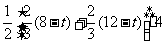 =
=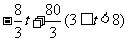
③ 当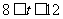 时,如图3,其重叠部分为△AGR,则AG=12-t ,
时,如图3,其重叠部分为△AGR,则AG=12-t , 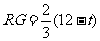
∴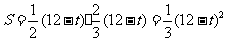
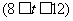
7.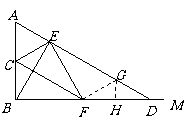 (黑龙江一模)如图,∠ABM为直角,点C为线段BA的中点,
(黑龙江一模)如图,∠ABM为直角,点C为线段BA的中点,
点D是射线BM上的一个动点(不与点B重合),连结AD,作
BE⊥AD,垂足为E,连结CE,过点E作EF⊥CE,交BD于F.
(1)求证:BF=FD;
(2)∠A在什么范围内变化时,四边形ACFE是梯形,并说明理由;
(3)∠A在什么范围内变化时,线段DE上存在点G,满足条件DG=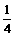 DA,并说明理由.
DA,并说明理由.
答案:
(1)在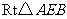 中,
中, ,
,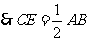 ,
,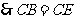 ,
, .
.
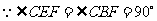 ,
,
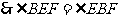 ,
,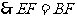 .
.
 ,
,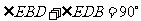 ,
,
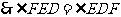 .
.
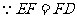 .
.
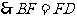 .(2)由(1)
.(2)由(1)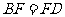 ,而
,而 ,
,
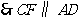 ,即
,即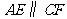 .
.
若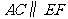 ,则
,则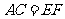 ,
,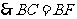 .
.
 ,
, .
.
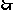 当
当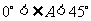 或
或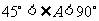 时,四边形
时,四边形 为梯形.
为梯形.
(3)作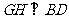 ,垂足为
,垂足为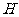 ,则
,则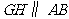 .
.
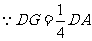 ,
,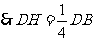 .
.
又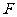 为
为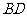 中点,
中点,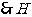 为
为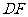 的中点.
的中点.
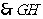 为
为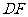 的中垂线.
的中垂线.
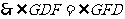 .
.
 点
点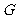 在
在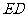 h上,
h上,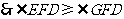 .
.
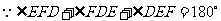 ,
,
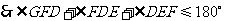 .
.
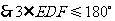 .
.
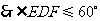 .
.
又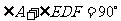 ,
,
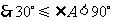 .
.
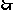 当
当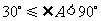 时,
时,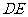 上存在点
上存在点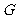 ,满足条件
,满足条件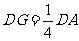 .
.
6.(2010年厦门湖里模拟)已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
答案:解:(1)解方程x2-10x+16=0得x1=2,x2=8
∵点B在x轴的正半轴上,点C在y轴的正半轴上,且OB<OC
∴点B的坐标为(2,0),点C的坐标为(0,8)
又∵抛物线y=ax2+bx+c的对称轴是直线x=-2
∴由抛物线的对称性可得点A的坐标为(-6,0)
(2)∵点C(0,8)在抛物线y=ax2+bx+c的图象上
∴c=8,将A(-6,0)、B(2,0)代入表达式,得
解得
∴所求抛物线的表达式为y=-x2-x+8
(3)依题意,AE=m,则BE=8-m,
 ∵OA=6,OC=8,∴AC=10
∵OA=6,OC=8,∴AC=10
∵EF∥AC ∴△BEF∽△BAC
∴= 即=
∴EF=
过点F作FG⊥AB,垂足为G,则sin∠FEG=sin∠CAB=
∴= ∴FG=·=8-m
∴S=S△BCE-S△BFE=(8-m)×8-(8-m)(8-m)
=(8-m)(8-8+m)=(8-m)m=-m2+4m
自变量m的取值范围是0<m<8
(4)存在.
理由:∵S=-m2+4m=-(m-4)2+8 且-<0,
∴当m=4时,S有最大值,S最大值=8
∵m=4,∴点E的坐标为(-2,0)
∴△BCE为等腰三角形.
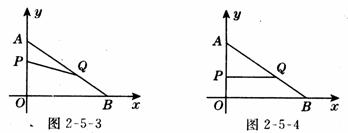
5.(2010年西湖区月考)如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
(1) 求直线AB的解析式;(2) 当t为何值时,△APQ与△AOB相似?
 (3) 当t为何值时,△APQ的面积为
(3) 当t为何值时,△APQ的面积为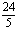 个平方单位?
个平方单位?
答案:(1)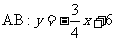 ;
;
(2)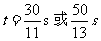 ;
;
 (3)
(3) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com