
1.已知集合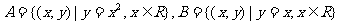 ,则集合
,则集合 中的元素个数为( )A.0个 B.1个 C.2个 D.无穷多个
中的元素个数为( )A.0个 B.1个 C.2个 D.无穷多个
22. 解:(Ⅰ)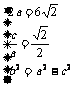

 所求椭圆M的方程为
所求椭圆M的方程为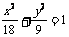 …3分
…3分
(Ⅱ)当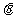 ≠
≠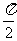 ,设直线AB的斜率为k = tan
,设直线AB的斜率为k = tan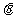 ,焦点F ( 3 , 0 ),则直线AB的方程为 y = k
( x – 3 ) 有
,焦点F ( 3 , 0 ),则直线AB的方程为 y = k
( x – 3 ) 有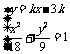
 ( 1 + 2k2 )x2
– 12k2x + 18( k2 – 1
) = 0
( 1 + 2k2 )x2
– 12k2x + 18( k2 – 1
) = 0
设点A ( x1
, y1 ) , B ( x2
, y2 ) 有x1 + x2
=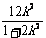 , x1x2 =
, x1x2 =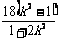
|AB| =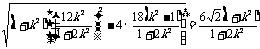
又因为k = tan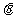 =
=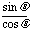 代入**式得 |AB| =
代入**式得 |AB| =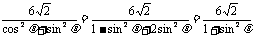
当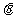 =
=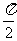 时,直线AB的方程为x = 3,此时|AB| =
时,直线AB的方程为x = 3,此时|AB| =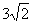
而当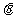 =
=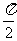 时,|AB| =
时,|AB| =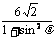 =
=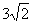
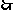 |AB| =
|AB| =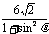
同理可得 |CD| =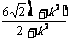 =
=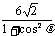
有|AB| + |CD| =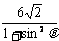 +
+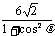 =
=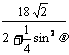
因为sin2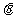 ∈[0,1],所以
当且仅当sin2
∈[0,1],所以
当且仅当sin2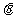 =1时,|AB|+|CD|有最小值是
=1时,|AB|+|CD|有最小值是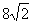
21. 解:(Ⅰ)当a=1时,对函数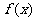 求导数,得
求导数,得
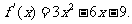 …2分
…2分
令 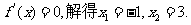
列表讨论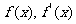 的变化情况:
的变化情况:
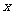 |
 |
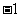 |
(-1,3) |
3 |
 |
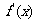 |
+ |
0 |
- |
0 |
+ |
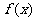 |
 |
极大值6 |
 |
极小值-26 |
 |
所以,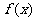 的极大值是
的极大值是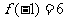 ,极小值是
,极小值是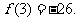 ………………6分
………………6分
(Ⅱ)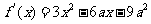 的图像是一条开口向上的抛物线,关于x=a对称.
的图像是一条开口向上的抛物线,关于x=a对称.
若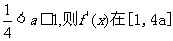 上是增函数,从而
上是增函数,从而
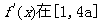 上的最小值是
上的最小值是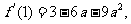 最大值是
最大值是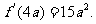
由 于是有
…………8分
于是有
…………8分
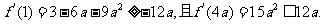
由 ………10分
………10分
所以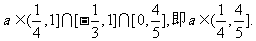
若a>1,则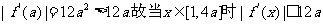 不恒成立.
不恒成立.
所以使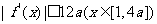 恒成立的a的取值范围是
恒成立的a的取值范围是 ………………12分
………………12分
18.解:(1) 设从甲、乙、丙三台机床加工的零件中任取一件是一等品为事件A,B,C , 则 P(A)=0.7, P(B)=0.6, P(C)=0.8
从甲、乙、丙加工的零件中各取一件检验,至少有一件一等品的概率为
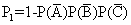 =1-0.3×0.4×0.2=0.976
4分
=1-0.3×0.4×0.2=0.976
4分
(2) 将三台机床加工的零件混合到一起,从中任意的抽取一件检验,它是一等品的概率为 P2=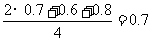 8分
8分
 (3)P(X=4)=
(3)P(X=4)= ×0.74=0.2401, P(X=3)=
×0.74=0.2401, P(X=3)=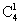 ×0.3×0.73=0.4116.
×0.3×0.73=0.4116.
故所求概率为0.2401+0.4116=0.6517
解:(1)连接B1C,交BC1于点O,
19则O为B1C的中点, D为AC中点,
D为AC中点,
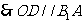 ,又
,又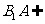 平面BDC1,
平面BDC1,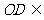 平面BDC1
平面BDC1
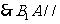 BDC1
3分
BDC1
3分
(2) 平面ABC,BC
平面ABC,BC AC,AA1//CC1,
AC,AA1//CC1,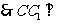 面ABC,
面ABC,
则BC 平面AC1,CC1
平面AC1,CC1 AC
AC
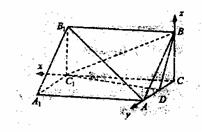
如图建系,则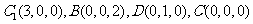
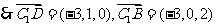
设平面C1DB的法向量为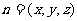 则
则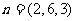
又平面BDC的法向量为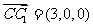
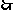 二面角C1-BD-C的余弦值:
二面角C1-BD-C的余弦值: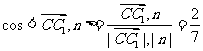 8分
8分
(3)设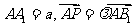 ,
,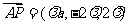
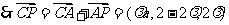 w
w
又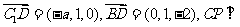 面BDC1,
面BDC1,
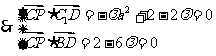 解得
解得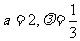
所以AA1=2,点P位置是在线段AB1上且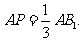 12分
12分
20:(1)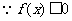 的解集有且只有一个元素
的解集有且只有一个元素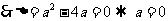 或
或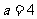
又由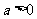 得
得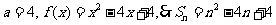
当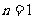 时,
时,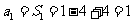 ;当
;当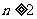 时,
时,
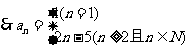
(2)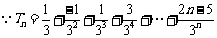 ①
①
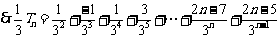 ②
②
由式①-或②得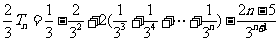
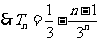 .
.
17.解:(1)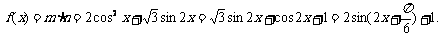
 ---------------2分
---------------2分
令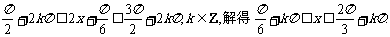
 --------------4分
--------------4分
(2)由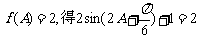 ,
,
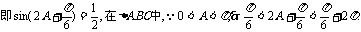
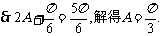 ------------6分
------------6分
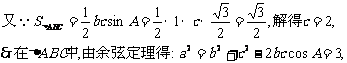
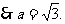 ---------8分
---------8分
由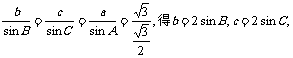
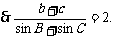 ---10分
---10分
22.设椭圆M: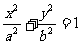 (a>b>0)的离心率为
(a>b>0)的离心率为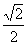 ,长轴长为
,长轴长为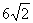 ,设过右焦点F倾
,设过右焦点F倾
斜角为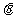 的直线交椭圆M于A,B两点。
的直线交椭圆M于A,B两点。
(Ⅰ)求椭圆M的方程;
(2)设过右焦点F且与直线AB垂直的直线交椭圆M于C,D,求|AB| + |CD|的最小值。
保定一中2009-2010届高三数学试卷(文)
21. (本小题12分)已知函数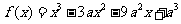 .
.
(1)
设 ,求函数
,求函数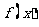 的极值;
的极值;
(2) 若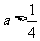 ,且当
,且当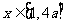 时,
时,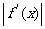
 12a恒成立,试确定
12a恒成立,试确定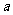 的取值范围.
的取值范围.
20. 已知二次函数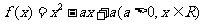 ,不等式
,不等式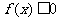 的解集有且只有一个元素,设数列
的解集有且只有一个元素,设数列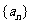 的前
的前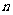 项和
项和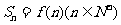
(1)求数列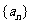 的通项公式;
的通项公式;
(2)设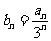 ,求数列
,求数列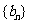 的前
的前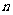 项和
项和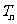 .
.
19.(本小题满分12分)
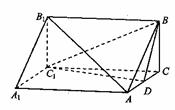 如图,三棱柱ABC-A1B1C1中,AA1
如图,三棱柱ABC-A1B1C1中,AA1 面ABC,BC
面ABC,BC AC,BC=AC=2,D为AC的中点。
AC,BC=AC=2,D为AC的中点。
(1)求证:AB1//面BDC1;
(2)若AA1=3,求二面角C1-BD-C的余弦值。
(3)若在线段AB1上存在点P,使得CP 面BDC1,试求AA1的长及点P的位置。
面BDC1,试求AA1的长及点P的位置。
18.甲、乙、丙三台机床各自独立的加工同一种零件,已知甲、乙、丙三台机床加工的零件是一等品的概率分别为0.7、0.6、0.8,乙、丙两台机床加工的零件数相等,甲机床加工的零件数是乙机床加工的零件数的二倍.
(1)从甲、乙、丙加工的零件中各取一件检验,求至少有一件一等品的概率;
(2)将三台机床加工的零件混合到一起,从中任意的抽取一件检验,求它是一等品的概率;
(3)将三台机床加工的零件混合到一起,从中任意的抽取4件检验,求一等品的个数不少于3个的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com