
15.已知抛物线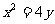 的焦点为F,准线与y轴的交点为M,N为抛物线上的一点,且
的焦点为F,准线与y轴的交点为M,N为抛物线上的一点,且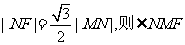 。
。
14.某企业职工的月工资数统计如下:
|
月工资数(元) |
10000 |
8000 |
5500 |
2500 |
1600 |
1200 |
900 |
600 |
500 |
|
得此工资人数 |
1 |
3 |
3 |
8 |
20 |
35 |
45 |
3 |
2 |
经计算,该企业职工工资的平均值为1565元,众数是900元,中位数是 元。如何选取该企业的月工资代表数呢?企业法人主张用平均值,职工代表主张用众数,监管部门主张用中位数。
请你站在其中一立场说明理由: 。
13.观察下列各式并填空:1=1,2+3+4=9,3+4+5+6+7= ,4+5+6+7+8+9+10=49,…,由此可归纳出 =
。
=
。
24.(本小题满分10分)选修4-5不等式选讲
对于任意的实数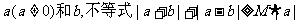 恒成立,记实数M的最大值是m。
恒成立,记实数M的最大值是m。
(1)求m的值;
(2)解不等式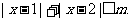
23.(本小题满分10分)选修4-2坐标系与参数方程
设直角坐标系原点与极坐标极点重合, x轴正半轴与极轴重合,若已知曲线C的极坐标方程为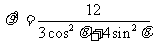 ,点F1、F2为其左、右焦点,直线l的参数方程为
,点F1、F2为其左、右焦点,直线l的参数方程为
(I)求直线l的普通方程和曲线C的直角坐标方程;
(II)求曲线C上的动点P到直线l的最大距离。
22.(本小题满分10分)选修4-1几何证明选讲
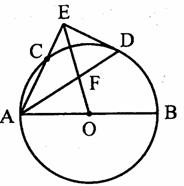
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F。
(I)求证:DE是⊙O的切线;
(II)若 的值.
的值.
21.(本小题满分12分)
已知函数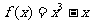
(I)设 是函数图象上的一点,求点M处的切线方程;
是函数图象上的一点,求点M处的切线方程;
(II)证明过点N(2,1)可以作曲线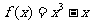 的三条切线。
的三条切线。
20.(本小题满分12分)
已知A、B分别为曲线C: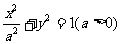 与x轴的左右两个交点,直线l过点B且x轴垂直,M为l上的一点,连结AM交曲线C于点T。
与x轴的左右两个交点,直线l过点B且x轴垂直,M为l上的一点,连结AM交曲线C于点T。
(I)当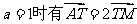 ,求点T坐标 ;
,求点T坐标 ;
(II)点M在x轴上方,若 的面积为2,当
的面积为2,当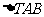 的面积的最大值为
的面积的最大值为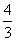 时,求曲线C的离心率e的取值范围。
时,求曲线C的离心率e的取值范围。
19.(本题满分12分)
如图,三棱锥S-ABC中,AB⊥BC,D、E分别为AC、BC的中点,SA=SB=SC。
(1)求证:BC⊥平面SDE;
(2)若AB=BC=2,SB=4,求三棱锥S-ABC的体积。

18.(本题满分12分)
一汽车厂生产A、B、C三类轿车,每类轿车有豪华型和标准型两种型号,某月生产情况如下表(单位:辆)
|
|
轿车A |
轿车B |
轿车C |
|
舒适型 |
100 |
150 |
x |
|
标准型 |
300 |
450 |
600 |
按分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(I)求x的值;
(I)列出所有基本事件,并求出至少有一辆是豪华型轿车的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com