
21.(12分)如图,已知四棱柱 的棱长都为
的棱长都为 ,底面
,底面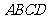 是菱形,且
是菱形,且 ,侧棱
,侧棱 ,
, 为棱
为棱 的中点,
的中点, 为线段
为线段 的中点.
的中点.
 (Ⅰ)求证:平面
(Ⅰ)求证:平面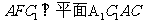 ;
;
(Ⅱ)求三棱锥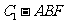 的体积.
的体积.
20. (12分)如图,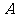 ,
,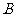 ,
,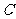 ,
,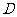 为空间四点,且
为空间四点,且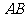
 ,
,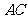

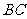

 .等边三角形
.等边三角形 以
以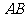 为轴转动.
为轴转动.
 (Ⅰ)当平面
(Ⅰ)当平面
 平面
平面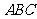 时,求
时,求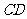 ;
;
(Ⅱ)当△ 转动时,是否总有
转动时,是否总有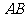

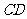 ?证明你的结论.
?证明你的结论.
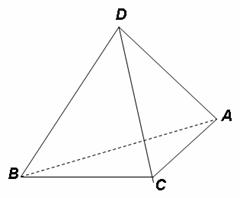
19、 (12分)如图:正四面体S-ABC中,棱长是a,如果E,F分别是SC,AB的中点,那么求异面直线EF与SA所成的角。
(12分)如图:正四面体S-ABC中,棱长是a,如果E,F分别是SC,AB的中点,那么求异面直线EF与SA所成的角。
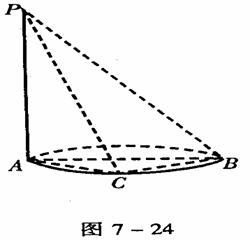
18.(12分)如图7-24,PA⊥⊙O所在平面,AB为底面圆的直径,C为下底面圆周上一点,求证:平面PBC⊥平面PAC
17、(12分)已知正方体 ,
, 是底
是底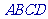 对角线的交点.
对角线的交点.
 求证:
求证: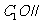 面
面 ;
;
16.在空间,有四个命题,①有两组对边相等的四边形是平行四边形 ②四边相等的四边形是菱形③平行于同一条直线的两直线平行④有两边及其夹角对应的两个三角形全等。其中正确的命题的序号是
15.已知平面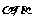 和直线,给出条件:①
和直线,给出条件:① ;②
;②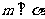 ;③
;③ ;④
;④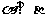 ;⑤
;⑤ .则当满足条件 时,有
.则当满足条件 时,有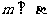 成立;(填所选条件的序号)
成立;(填所选条件的序号)
14.正四面体中,则其侧面与底面的二面角的余弦值等于
13.已知球内接正方体的表面积为6,则球的表面积等于 .
12、正三棱锥底面边长为a,侧棱与底面成60°角,则一个侧面在底面的射影面积为( )。
A. 3a2 B. 2a2 C. 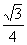 a2 D.
a2 D. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com