11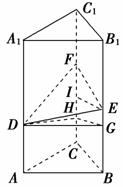．一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上．已知正三棱柱的底面边长为2，求该三角形的斜边长．

解：如图，正三棱柱ABC－A₁B₁C₁中，△ABC为正三角形，边长为2，△DEF为等腰直角三角形，DF为斜边，设DF长为x，则DE＝EF＝x，作DG⊥BB₁，HG⊥CC₁，EI⊥CC₁，

则EG＝＝，FI＝＝，FH＝FI+HI＝FI+EG＝2，在Rt△DHF中，DF²＝DH²+FH²，即x²＝4+(2)²，解得x＝2.即该三角形的斜边长为2.

10．一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱，这个四棱锥的底面为正方形，且底面边长与各侧棱长相等，这个三棱锥的底面边长与各侧棱长也都相等．设四棱锥、三棱锥、三棱柱的高分别为h₁，h₂，h₃，求h₁∶h₂∶h₃的值．

解：选依题意，四棱锥为正四棱锥，三棱锥为正三棱锥，且棱长均相等，设为a，h₂＝h₃，h₁＝ ＝a，h₂＝ ＝a，

故h₁∶h₂∶h₃＝∶2∶2.

9．(2008年高考江西卷)如图(1)，一个正四棱柱形的密闭容器水平放置，其底部镶嵌了同底的正四棱锥形实心装饰块，容器内盛有a升水时，水面恰好经过正四棱锥的顶点P.如果将容器倒置，水面也恰好过点P(图(2))

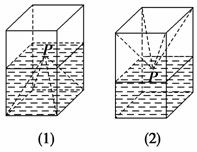
有下列四个命题：

A．正四棱锥的高等于正四棱柱高的一半

B．将容器侧面水平放置时，水面也恰好过点P

C．任意摆放该容器，当水面静止时，水面都恰好经过点P

D．若往容器内再注入a升水，则容器恰好能装满．

其中真命题的代号是：______(写出所有真命题的代号)．

解析：设正四棱柱底面边长为b，高为h₁，正四棱锥高为h₂，则原题图(1)中水的体积为b²h₂－b²h₂＝b²h₂，

图(2)中水的体积为b²h₁－b²h₂＝b²(h₁－h₂)，

所以b²h₂＝b²(h₁－h₂)，所以h₁＝h₂，故A错误，D正确．

对于B，当容器侧面水平放置时，P点在长方体中截面上，又水占容器内空间的一半，所以水面也恰好经过P点，故B正确．对于C，假设C正确，当水面与正四棱锥的一个侧面重合时，经计算得水的体积为b²h₂>b²h₂，矛盾，故C不正确．答案：BD

8．如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰，以下四个命题中，假命题是________．

①等腰四棱锥的腰与底面所成的角都相等

②等腰四棱锥的侧面与底面所成的二面角都相等或互补

③等腰四棱锥的底面四边形必存在外接圆

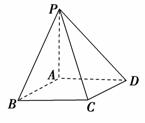④等腰四棱锥的各顶点必在同一球面上

解析：①如图，∵SA=SB=SC=SD，∴∠SAO=∠SBO=∠SCO=∠SDO，即等腰四棱锥腰与底面所成的角相等，正确；②等腰四棱锥的侧面与底面所成的二面角相等或互补不一定成立；③如图，由SA=SB=SC=SD得OA=OB=OC=OD，即等腰四棱锥的底面四边形存在外接圆，正确；④等腰四棱锥各顶点在同一个球面上，正确．故选②.答案：②

7．过半径为2的球O表面上一点A作球O的截面，若OA与该截面所成的角是60°，则该截面的面积是________．

解析：设截面的圆心为O′，由题意得：∠OAO′＝60°，O′A＝1，S＝π·1²＝π.答案：π

6．下列结论正确的是　　

①各个面都是三角形的几何体是三棱锥

②以三角形的一条边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫圆锥

③棱锥的侧棱长与底面多边形的边长相等，则该棱锥可能是正六棱锥

④圆锥的顶点与底面圆周上的任意一点的连线都是母线

解析：①错误．如图(1)所示，由两个结构相同的三棱锥叠放在一起构成的几何体，各面都是三角形，但它不是棱锥．

②错误．如图(2)(3)所示，若△ABC不是直角三角形，或是直角三角形但旋转轴不是直角边，所得的几何体都不是圆锥．

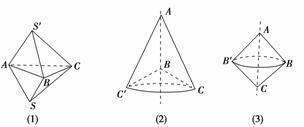
③错误．若六棱锥的所有棱长都相等，则底面多边形是正六边形．由几何图形知，若以正六边形为底面，侧棱长必然要大于底面边长．

④正确．答案：④

5．给出以下命题：①底面是矩形的四棱柱是长方体；②直角三角形绕着它的一边旋转一周形成的几何体叫做圆锥；③四棱锥的四个侧面可以都是直角三角形．其中说法正确的是__________．

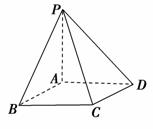解析：命题①不是真命题，因为底面是矩形，若侧棱不垂直于底面，这时四棱柱是斜四棱柱；命题②不是真命题，直角三角形绕着它的一条直角边旋转一周形成的几何体叫做圆锥，如果绕着它的斜边旋转一周，形成的几何体则是两个具有共同底面的圆锥；命题③是真命题，如图所示，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，则可以得到四个侧面都是直角三角形．故填③.

答案：③

4．(2009年高考安徽卷)对于四面体ABCD，下列命题正确的是________．

①相对棱AB与CD所在的直线是异面直线；

②由顶点A作四面体的高，其垂足是△BCD三条高线的交点；

③若分别作△ABC和△ABD的边AB上的高，则这两条高的垂足重合；

④任何三个面的面积之和都大于第四个面的面积；

⑤分别作三组相对棱中点的连线，所得的三条线段相交于一点．

解析：②中的四面体如果对棱垂直，则垂足是△BCD的三条高线的交点；③中如果AB与CD垂直，则两条高的垂足重合．答案：①④⑤

3.关于如图所示几何体的正确说法为________．

①这是一个六面体　②这是一个四棱台

③这是一个四棱柱　④这是一个四棱柱和三棱柱的组合体　

⑤这是一个被截去一个三棱柱的四棱柱

答案：①②③④⑤

2．下面是关于三棱锥的四个命题：

①底面是等边三角形，侧面与底面所成的二面角都相等的三棱锥是正三棱锥．

②底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥．

③底面是等边三角形，侧面的面积都相等的三棱锥是正三棱锥．

④侧棱与底面所成的角都相等，且侧面与底面所成的二面角都相等的三棱锥是正三棱锥．

其中，真命题的编号是______．(写出所有真命题的编号)

解析：对于①，设四面体为D－ABC，过棱锥顶点D作底面的垂线DE，过E分别作AB，BC，CA边的垂线，其垂足依次为F，G，H，连结DF，DG，DH，则∠DFE，∠DGE，∠DHE分别为各侧面与底面所成的角，所以∠DFE＝∠DGE＝∠DHE，于是有FE＝EG＝EH，DF＝DG＝DH，故E为△ABC的内心，又因△ABC为等边三角形，所以F，G，H为各边的中点，所以△AFD≌△BFD≌△BGD≌△CGD≌△AHD，故DA＝DB＝DC，故棱锥为正三棱锥．所以为真命题．对于②，侧面为等腰三角形，不一定就是侧棱为两腰，所以为假命题．对于③，面积相等，不一定侧棱就相等，只要满足斜高相等即可，所以为假命题．对于④，由侧棱与底面所成的角相等，可以得出侧棱相等，又结合①知底面应为正三角形，所以为真命题．综上，①④为真命题．答案：①④