
12.下列离子方程式书写正确的是
A.将少量SO2气体通入NaClO溶液中
SO2 +2ClO-+H2O = SO32-+2HClO
B.向KHSO4溶液中加入Ba(OH)2溶液至所得溶液的pH=7
Ba2+ +OH-+ H++ SO42- = BaSO4↓+ 2H2O
C.向Ca(H2PO4)2溶液中滴入过量的NaOH溶液
3Ca2+ + 6H2PO4-+12OH-= Ca3(PO4)2↓+ 4PO43-+12H2O
D.112mL(标况)Cl2通入10mL1mol/L的FeBr2溶液中
2Fe2+ + 4Br-+3Cl2 = 2Fe3+ + 6Cl-+2Br2
11.下列有关实验操作说法中,正确的是
①用pH试纸测得氯水的pH为2 ②用量筒、试管胶头滴管、玻璃棒、蒸馏水和pH试纸,可鉴别pH相等的硫酸和醋酸 ③分液时,分液漏斗中下层液体从下口放出,上层液体从上口倒出 ④用碱式滴定管量取25.00mL溴水 ⑤可用渗析的方法除去淀粉中混有的少量的NaCl杂质 ⑥在进行过滤操作时,为了加快速率,可用玻璃棒不断搅拌过滤器中液体
A.①③⑤ B.②③⑤ C.③④⑤ D.①③④⑥
10.一定温度下,mg下列物质在足量的氧气中充分燃烧后,产物与足量的过氧化钠充分反应,过氧化钠增加了ng,且n<m,符合此要求的物质是
①H2 ②CO ③CO和H2的混合物 ④C12H22O11 ⑤HCOOH
A.④ B.①② C.①②③ D.⑤
9.将固体NH4I置于密闭容器中,在一定温度下发生下列反应:
①NH4I(s) NH3(g)+HI(g);②2HI(g)
NH3(g)+HI(g);②2HI(g) H2(g)+I2(g)。
H2(g)+I2(g)。
达到平衡时,c(H2)=0.5mol·L-1,c(HI)=4mol·L-1,则此温度下反应①的平衡常数为
A.9 B.16 C.20 D.25
8.阿伏加德罗常数约为6.02×1023mol-1,下列说法中一定正确的是
A、1L1 mol·L-1的HAc溶液中含有氢离子数约为6.02×1023
B、18g D2O(重水)完全电解,转移的电子数约为6.02×1023
C、22.4LNO2气体,所含氧原子数约为2×6.02×1023
D、14g乙烯和丙烯的混合物中,含有共用电子对数目约为3×6.02×1023
7.下列物质中不能通过置换反应生成的是
A.Al2O3 B.F2 C.Fe3O4 D.C
21.本题有⑴、⑵、⑶三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.
(1)曲线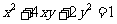 在二阶矩阵
在二阶矩阵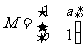 的作用下变换为曲线
的作用下变换为曲线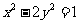 ,
,
①求实数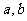 的值;②求
的值;②求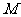 的逆矩阵
的逆矩阵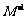 .
.
(2)在曲线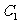 :
: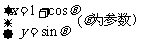 ,在曲线
,在曲线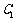 求一点,使它到直线
求一点,使它到直线 :
: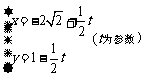 的距离最小,并求出该点坐标和最小距离.
的距离最小,并求出该点坐标和最小距离.
(3)设函数 .
.
①当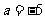 时,求函数
时,求函数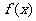 的定义域;②若函数
的定义域;②若函数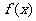 的定义域为
的定义域为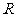 ,求
,求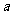 的取值范围.
的取值范围.
20.(本小题满分14分)已知函数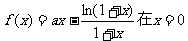 处取得极值.
处取得极值.
(1)求实数a的值,并判断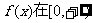 上的单调性;
上的单调性;
(2)若数列 满足
满足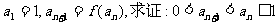 ;
;
(3)在(2)的条件下,记
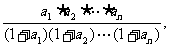
求证: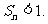
19.(本小题满分13分)
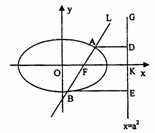
如图,已知直线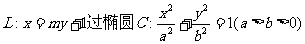 的右焦点F,且交椭圆C于A,B两点,点A,F,B在直线
的右焦点F,且交椭圆C于A,B两点,点A,F,B在直线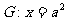 上的射影依次为点D,K,E.
上的射影依次为点D,K,E.
 (1)若抛物线
(1)若抛物线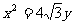 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程;
(2)对于(1)中的椭圆C,若直线L交y轴于点M,且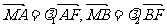 ,当m变化时,求
,当m变化时,求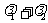 的值;
的值;
(3)连接AE,BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标并给予证明;否则说明理由.
18.(本小题满分13分)
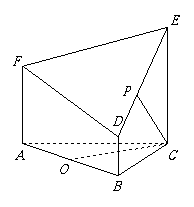 如图所示的几何体是由以等边三角形
如图所示的几何体是由以等边三角形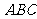 为底面的棱柱被平面
为底面的棱柱被平面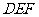 所截而得,已知
所截而得,已知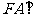 平面
平面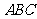 ,
,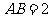 ,
,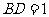 ,
,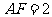 ,
,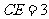 ,
,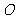 为
为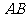 的中点.
的中点.
(Ⅰ)求证: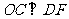 ;
;
(Ⅱ)求平面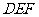 与平面
与平面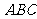 相交所成锐角二面角的余弦值;
相交所成锐角二面角的余弦值;
(Ⅲ)在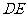 上是否存在一点
上是否存在一点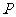 ,使
,使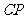
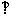 平面
平面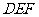 ?如果存在,求出
?如果存在,求出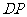 的长;若不存在,说明理由.
的长;若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com