
1.下列叙述中符合物理学史实的是 ( )
A.奥斯特发现了电磁感应现象并给出了电磁感应定律
B.库仑总结并确认了真空中两个点电荷之间的相互作用规律
C.牛顿总结了万有引力定律并测出了引力常量
D.伽利略根据客观实验数据得出力不是维持物体运动的原因的结论
24.(本小题满分10分)选修4-5:不等式选讲
设函数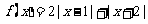 .
.
(Ⅰ)求不等式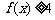 的解集;
的解集;
(Ⅱ)若不等式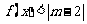 的解集是非空的集合,求实数
的解集是非空的集合,求实数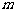 的取值范围.
的取值范围.
23.(本小题满分10分)选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的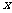 轴的正半轴重合.直线
轴的正半轴重合.直线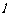 的参数方程是
的参数方程是 (
(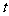 为参数),曲线
为参数),曲线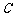 的极坐标方程为
的极坐标方程为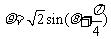 .
.
(Ⅰ)求曲线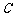 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线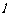 与曲线
与曲线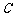 相交于
相交于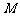 ,
,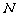 两点,求M,N两点间的距离.
两点,求M,N两点间的距离.
题计入总分,满分10分. 请将答题的过程写在答题卷中指定的位置)
22.(本小题满分10分)选修4-1:几何证明选讲
如图,已知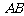 是
是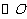 的直径,
的直径,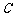 ,
,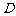 是
是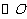 上两点,
上两点,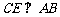 于
于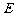 ,
,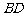 交
交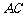 于
于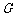 ,交
,交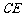 于
于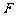 ,
,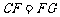 .
.
(Ⅰ)求证: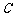 是
是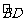 的中点;
的中点;
(Ⅱ)求证: .
.

21.(本小题满分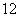 分)
分)
已知函数 (
(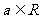 ).
).
(Ⅰ)当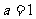 时,求
时,求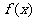 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;
(Ⅱ)若在区间(1,+∞)上,函数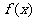 的图象恒在直线
的图象恒在直线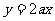 下方,求
下方,求 的取值范围.
的取值范围.
20.(本小题满分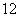 分)
分)
在平面直角坐标系中,已知两个定点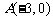 和
和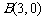 .动点
.动点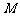 在
在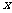 轴上的射影是
轴上的射影是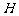 (
(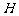 随
随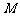 移动而移动),若对于每个动点M总存在相应的点
移动而移动),若对于每个动点M总存在相应的点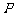 满足
满足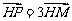 ,且
,且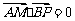 .
.
(Ⅰ)求动点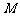 的轨迹
的轨迹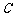 的方程;
的方程;
(Ⅱ)设过定点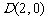 的直线
的直线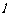 (直线
(直线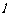 与
与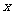 轴不重合)交曲线
轴不重合)交曲线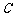 于
于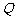 ,
,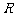 两点,求证:直线
两点,求证:直线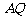 与直线
与直线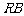 交点总在某直线
交点总在某直线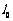 上.
上.
19.(本小题满分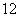 分)
分)
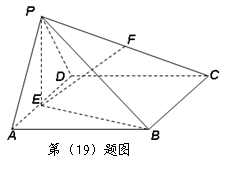
在四棱锥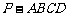 中,平面
中,平面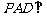 平面
平面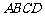 ,△
,△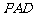 是等边三角形,底面
是等边三角形,底面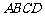 是边长为
是边长为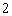 的菱形,
的菱形,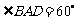 ,
,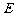 是
是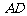 的中点,
的中点,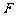 是
是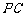 的中点.
的中点.
(Ⅰ)求证: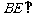 平面
平面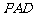 ;
;
(Ⅱ) 求证: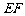 ∥平面
∥平面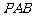 ;
;
(Ⅲ)
求直线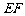 与平面
与平面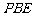 所成角的余弦值.
所成角的余弦值.
18.(本小题满分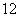 分)
分)
某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
(Ⅰ)求甲、乙两同学都被抽到的概率,其中甲为A类同学,乙为B类同学;
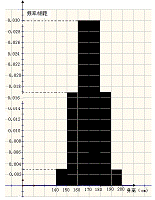
(Ⅱ) 测得该年级所抽查的100名同学身高(单位:厘米) 频率分布直方图如右图:
(ⅰ) 统计方法中,同一组数据常用该组区间的中点值(例如区间 的中点值为165)作为代表.据此,计算这100名学生身高数据的期望
的中点值为165)作为代表.据此,计算这100名学生身高数据的期望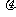 及标准差
及标准差 (精确到0.1);
(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,据此,估计该年级身高在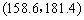 范围中的学生的人数
.
范围中的学生的人数
.
(Ⅲ) 如果以身高达170cm作为达标的标准,对抽取的100名学生,得到下列联表:
体育锻炼与身高达标2×2列联表
|
|
身高达标 |
身高不达标 |
总计 |
|
积极参加体育锻炼 |
40 |
|
|
|
不积极参加体育锻炼 |
|
15 |
|
|
总计 |
|
|
100 |
(ⅰ)完成上表;
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
参考公式:K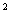 =
=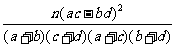 ,参考数据:
,参考数据:
P(K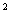  k) k) |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
|
k |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
]
17.(本小题满分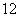 分)
分)
设数列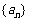 的前
的前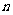 项和为
项和为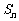 ,且
,且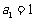 ,
,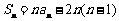 .
.
 (Ⅰ)求
(Ⅰ)求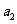 ,
,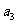 ,
,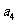 ,并求出数列
,并求出数列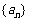 的通项公式;
的通项公式;
(Ⅱ)设数列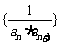 的前
的前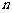 项和为
项和为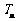 ,试求
,试求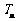 的取值范围.
的取值范围.
16.用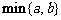 表示
表示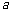 ,
,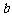 两个数中的最小值,设
两个数中的最小值,设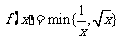 (
(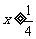 ),则由函数
),则由函数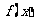
的图象,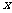 轴与直线
轴与直线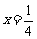 和直线
和直线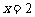 所围成的封闭图形的面积为_____
所围成的封闭图形的面积为_____
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com