
11、 一定条件下,对于可逆反应X(g)+3Y(g) 2Z(g),若X、Y、Z的起始浓度分别为C1、C2、C3(均不为零),到达平衡时,X、Y、Z的浓度分别为0.1 mol·L-1
、0.3 mol·L-1、0.08 mol·L-1,则下列判断正确的是
一定条件下,对于可逆反应X(g)+3Y(g) 2Z(g),若X、Y、Z的起始浓度分别为C1、C2、C3(均不为零),到达平衡时,X、Y、Z的浓度分别为0.1 mol·L-1
、0.3 mol·L-1、0.08 mol·L-1,则下列判断正确的是
A、C1:C2=1:3 B、平衡时,Y和Z的生成速率之比为2:3
C、X、Y的转化率相等 D、C1的取值范围为0.04 mol·L-1 <C1<0.14 mol·L-1
9.一定温度下,向质量分数为 a的乙腈(CH3CN)溶液中加入等体积水,所得溶液中乙腈质量分数为 0.4a ,则乙腈的密度(ρ1)与水的密度(ρ2)关系是
A.ρ1 >ρ2 B.ρ1 <ρ2
C.ρ1 =ρ2 D.无法确定
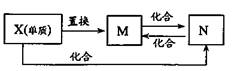 10、右图中,M、N为含X元素的常见化合物。
10、右图中,M、N为含X元素的常见化合物。
则X元素为
A.Fe或C B.Cu或Fe
C.N或S D.C或Al
8.向BaCl2溶液中通入SO2至饱和,此过程看不到现象。再向溶液中加入一种物质,溶液变浑浊。加入的这种物质不可能是( )
A、FeCl3溶液 B、AlCl3溶液 C、Na2S溶液 D、AgNO3溶液
7.下列叙述正确的是
A、目前加碘食盐中主要添加的KIO3 B、日常生活中无水乙醇常用于杀菌消毒
C、绿色食品是不含任何化学物质的食品
D、在空气质量日报中CO2含量高于空气污染指数
23.(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分8分.
定义:如果数列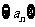 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称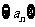 为“三角形”数列.对于“三角形”数列
为“三角形”数列.对于“三角形”数列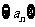 ,如果函数
,如果函数 使得
使得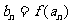 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称 是数列
是数列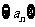 的“保三角形函数”,
的“保三角形函数”,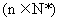 .
.
(1)已知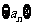 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若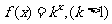 是数列
是数列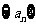 的“保三角形函数”,求k的取值范围;
的“保三角形函数”,求k的取值范围;
(2)已知数列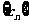 的首项为2010,
的首项为2010,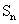 是数列
是数列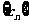 的前n项和,且满足
的前n项和,且满足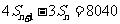 ,证明
,证明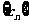 是“三角形”数列;
是“三角形”数列;
(3) [文科] 若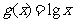 是(2)中数列
是(2)中数列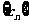 的“保三角形函数”,问数列
的“保三角形函数”,问数列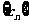 最多有多少项?
最多有多少项?
[理科] 根据“保三角形函数”的定义,对函数 ,
,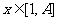 ,和数列1,
,和数列1,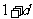 ,
, (
(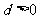 )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由.
2010年四区(杨浦、静安、青浦、宝山)联合高考模拟
22. (本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分4分,第3小题满分8分.
已知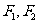 为椭圆
为椭圆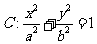 ,
,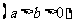 的左右焦点,
的左右焦点,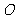 是坐标原点,过
是坐标原点,过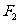 作垂直于
作垂直于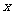 轴的直线
轴的直线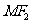 交椭圆于
交椭圆于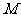 ,设
,设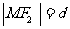 .
.
(1)证明: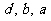 成等比数列;
成等比数列;
(2)若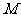 的坐标为
的坐标为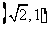 ,求椭圆
,求椭圆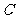 的方程;
的方程;
(3)[文科] 在(2)的椭圆中,过 的直线
的直线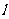 与椭圆
与椭圆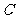 交于
交于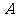 、
、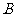 两点,若
两点,若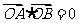 ,求直线
,求直线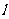 的方程.
的方程.
[理科] 在(2)的椭圆中,过 的直线
的直线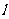 与椭圆
与椭圆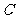 交于
交于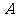 、
、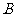 两点,若椭圆
两点,若椭圆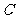 上存在点
上存在点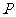 ,使得
,使得
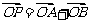 ,求直线
,求直线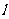 的方程.
的方程.
21.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
[文科]已知平面向量 ,
,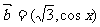 ,函数
,函数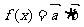 .
.
(1)写出函数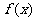 的单调递减区间;
的单调递减区间;
(2)设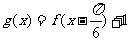 ,求直线
,求直线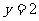 与
与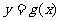 在闭区间
在闭区间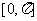 上的图像的所有交点坐标.
上的图像的所有交点坐标.
[理科] 已知平面向量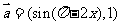 ,
,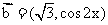 ,函数
,函数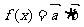 .
.
(1)写出函数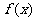 的单调递减区间;
的单调递减区间;
(2)设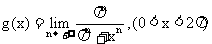 ,求函数
,求函数 与
与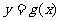 图像的所有交点坐标.
图像的所有交点坐标.
20. (本题满分14分)本题共有2个小题,第1小题满分5分,第2小题满分9分.
把水放在温度为 ℃的空气中冷却,若水原来的温度是
℃的空气中冷却,若水原来的温度是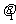 ℃
℃ ,
,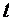 分钟后物体温度
分钟后物体温度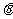 ℃可由公式
℃可由公式 求得,其中,
求得,其中,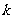 是由不同盛水的容器所确定的正常量.
是由不同盛水的容器所确定的正常量.
(1)若室温为20℃,往某容器中倒入98℃的热水,一小时后测得水温为71.2℃,求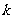 的值;(精确到0.001)
的值;(精确到0.001)
(2)若一保温杯的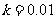 ,往该保温杯中倒入100℃的开水,经过2.5小时测得水温为40℃,求此时的室内温度(假设室内恒温,精确到0.1℃).
,往该保温杯中倒入100℃的开水,经过2.5小时测得水温为40℃,求此时的室内温度(假设室内恒温,精确到0.1℃).
19. (本题满分12分)
(本题满分12分)
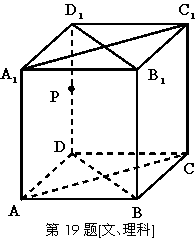
[文科]已知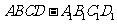 是底面为菱形的直四棱柱,
是底面为菱形的直四棱柱,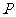 是棱
是棱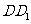 的中点,
的中点,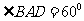 ,底面边长为2,四棱柱的体积为
,底面边长为2,四棱柱的体积为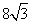 ,求异面直线
,求异面直线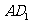 与
与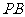 所成的角大小.(结果用反三角函数值表示)
所成的角大小.(结果用反三角函数值表示)
[理科]已知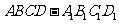 是底面为菱形的直四棱柱,
是底面为菱形的直四棱柱,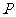 是棱
是棱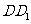 的中点,
的中点,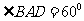 ,底面边长为2,若
,底面边长为2,若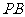 与平面
与平面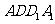 成
成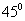 角,求点
角,求点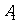 到平面
到平面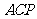 的距离.
的距离.
18.[文科] 已知函数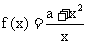 ,
,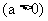 ,
,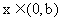 ,则下列判断正确的是( ).
,则下列判断正确的是( ).
(A) 当 时,
时,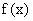 的最小值为
的最小值为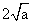 ;
;
(B) 当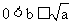 时,
时,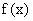 的最小值为
的最小值为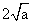 ;
;
(C) 当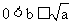 时,
时,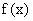 的最小值为
的最小值为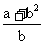 ;
;
(D) 对任意的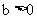 ,
,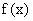 的最小值均为
的最小值均为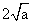 .
.
[理科] 设函数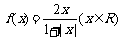 ,区间
,区间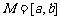 ,
,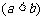 ,集合
,集合 ,则使
,则使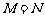 成立的实数对
成立的实数对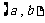 有( ).
有( ).
(A) 3对; (B) 5对; (C) 1对; (D) 无数对.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com