
1.亮氨酸的分子式是C6H13NO2,其R基为
A.-C4H9 B.-C5H9 C.-C6H13 D.-C4H8
9.如图所示,在 平面内的第III象限中有沿-y方向的匀强电场,场强大小为E。只第I和第II象限有匀强磁场,磁场方向垂直于坐标平面向里,有一质量为m,电荷量为e的电子,从y轴的P点以初速度v0垂直于电场方向进入电场,P点坐标为
平面内的第III象限中有沿-y方向的匀强电场,场强大小为E。只第I和第II象限有匀强磁场,磁场方向垂直于坐标平面向里,有一质量为m,电荷量为e的电子,从y轴的P点以初速度v0垂直于电场方向进入电场,P点坐标为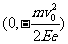 ,经电场偏转后,与x轴负半轴成一定角度进入磁场,设磁感应强度B的大小为
,经电场偏转后,与x轴负半轴成一定角度进入磁场,设磁感应强度B的大小为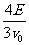 。求:
。求:
 (1)电子经过x轴负半轴的坐标和此时速度方向与-x
(1)电子经过x轴负半轴的坐标和此时速度方向与-x
轴方向的夹角;
(2)电子再次经过y轴负半轴的坐标。
解:(15分)
(1)电子在电场做类平抛运动,加速度为 (1分)
(1分)
令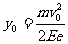 ,则时间为
,则时间为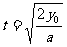 (1分)
(1分)
电子经过x轴负半轴的坐标 (2分)
(2分)
由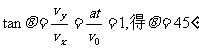
故速度方向与-x轴方向成45°(2分)
(2)电子进入磁场速度应为 ,进入磁场方向与x轴负方向成45°(1分)
,进入磁场方向与x轴负方向成45°(1分)
进入磁场所作圆周运动半径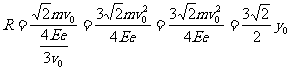 (2分)
(2分)
由几何关系可知轨迹与x轴两交点间距离为 (1分)
(1分)
 (1分)
(1分)
电子接着从B点做匀速直线运动,由对称性知与x轴负方向成45°(2分)
故再次经过y轴的坐标为 ,即与P点重合(2分)
,即与P点重合(2分)
8.如图所示,水平轨道上,轻弹簧左端固定,自然状态时右端位于P点.现用一质量m=0.1kg的小物块 (视为质点)将弹簧压缩后释放,物块经过P点时的速度v0=18m/s,经过水平轨道右端Q点后恰好沿半圆轨道的切线进入竖直固定的圆轨道,最后滑上质量M=0.9kg的长木板(木板足够长,物块滑上去不会从木板上掉下来).已知PQ间的距离l=1m,竖直半圆轨道光滑且半径R=1m,物块与水平轨道间的动摩擦因数µ1=0.15,与木板间的动摩擦因数µ2=0.2,木板与水平地面间的动摩擦因数µ3=0.01,取g=10m/s2.
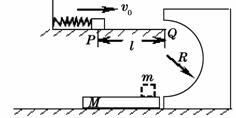 (1)判断物块经过Q点后能否沿圆周轨道运动;
(1)判断物块经过Q点后能否沿圆周轨道运动;
(2)求木板滑行的最大距离x.
解:(1)物块在PQ上运动的加速度
a1=-µ1g=-1.5m/s2 (1分)
进入圆周轨道时的速度为v
v2-v02=2a1l
得v2=v02+2a1l =321 m2/s2(1分)
 设物块刚离开Q点时,圆轨道对物块的压力为FN ,
设物块刚离开Q点时,圆轨道对物块的压力为FN ,
根据牛顿定律,有
FN+mg=m
FN =m - mg=31.1N>0(2分)
- mg=31.1N>0(2分)
故物块能沿圆周轨道运动(1分)
(2)物块滑上木板时的速度为v1
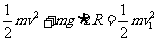
得v1=19m/s (2分)
物块滑上木板时的加速度为a2
a2=-µ2g=-2m/s2 (1分)
木板的加速度位a3
µ2mg-µ3(m+M)g=Ma3
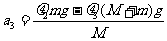 =
= m/s2
(2分)
m/s2
(2分)
设物块滑上木板经过时间t二者共速,
v1+a2t=a3t
t=9s (1分)
这时木板的位移
s1=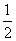 a3t2=4.5m
(1分)
a3t2=4.5m
(1分)
它们的共同速度
v2=a3t=1m/s (1分)
物块和木板一起减速的加速度a4=-µ3g=-0.1m/s2,
它们减速运动的位移s2= =5m (1分)
=5m (1分)
x=s1+s2=9.5m (1分)
7.如图所示,质量为m、电荷量为q的带电粒子,沿与水平面成θ=60°的方向匀速运动,进入垂直纸面向里的圆形匀强磁场区域后,从水平金属板M左端下边缘附近水平射出磁场,进入两平行金属板M、N间,恰好从N板右边缘飞出.已知匀强磁场的磁感应强度为B,方向垂直于纸面向里,两带电极板M、N长为l,间距为d,板间电压为U,不计粒子重力.
⑴分析判断极板M带正电还是带负电?
⑵求粒子在磁场中运动的速度大小;
⑶求粒子进入磁场时的入射点与离开磁场时的出射点之间的距离.
解: ⑴粒子在磁场中向右偏转,由左手定则可知,粒子带负电;粒子在电场中向下偏转, 所以M板带负电。(2分)
⑵设带电粒子进入电场时的初速度为v,则
 (3分)
(3分)
 解得
解得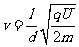 。(2分)
。(2分)
⑶设磁偏转的半径为R,则由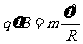
得 (2分)
(2分)
如图所示,粒子进入磁场时的入射点与离开磁场时的出射点间的距离
d=2Rsin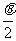 =2Rsin300=
=2Rsin300=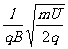 (2分)
(2分)
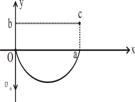
6.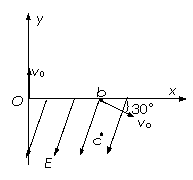 一质量为m、带电量为+q的粒子以速度v0从O点沿y轴正方向射入一圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从b处穿过x轴,速度方向与x轴正方向的夹角为30°,同时进入场强大小为大小为E,方向沿x轴负方向成60°角斜向下的匀强电场中,通过了b点正下方c点,如图所示,已知 b到O的距离为L,粒子的重力不计,试求:
一质量为m、带电量为+q的粒子以速度v0从O点沿y轴正方向射入一圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从b处穿过x轴,速度方向与x轴正方向的夹角为30°,同时进入场强大小为大小为E,方向沿x轴负方向成60°角斜向下的匀强电场中,通过了b点正下方c点,如图所示,已知 b到O的距离为L,粒子的重力不计,试求:
⑴磁感应强度B
⑵圆形匀强磁场区域的最小面积;
⑶c点到b点的距离
解.(1)粒子在磁场中受洛仑兹力作用,作匀速圆周运动,设其半径为R,据此并由题意知,粒子在磁场中的轨迹的圆心C必在x轴上,且b点在磁场区之外。过b沿速度方向作延长线,它与y轴相交于d点。作圆弧过O点与y轴相切,并且与bd相切,切点a即粒子离开磁场区的地点。这样也求得圆弧轨迹的圆心C,如图所示。
由图中几何关系得:L=3R (2分)
 由①、②求得
由①、②求得 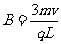 (2分)
(2分)
(2)要使磁场的区域有最小面积,则Oa应为磁场区域的直径,由几何关系知: 由②、④得
由②、④得  (2分)
(2分)
∴匀强磁场的最小面积为: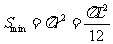 (2分)
(2分)
(3)带电粒子进入电场后,由于速度方向与电场力方向垂直,故做类平抛运动,由运动的合成知识有:s·sin30°=v0t(2分) s·cos30°=at2/2 (2分) 而a=qE/m
联立解得: 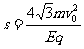 (2分)
(2分)
5.某课外小组设计了一种测定风速的装置,其原理如图所示,一个劲度系数k=120N/m,自然长度L0=1m弹簧一端固定在墙上的M点,另一端N与导电的迎风板相连,弹簧穿在光滑水平放置的电阻率较大的金属杆上,弹簧是不导电的材料制成的。迎风板面积S=0.5m2,工作时总是正对着风吹来的方向。电路的一端与迎风板相连,另一端在M点与金属杆相连。迎风板可在金属杆上滑动,且与金属杆接触良好。定值电阻R=1.0Ω,电源的电动势E=12V,内阻r=0.5Ω。闭合开关,没有风吹时,弹簧处于原长,电压表的示数U1=9.0V,某时刻由于风吹迎风板,电压表的示数变为U2=6.0V。(电压表可看作理想表)求:
 ⑴金属杆单位长度的电阻;
⑴金属杆单位长度的电阻;
⑵此时作用在迎风板上的风力;
解.设无风时金属杆接入电路的电阻为R1,风吹时接入电路的电阻为R2,由题意得
⑴无风时:U1=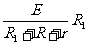 得R1=4.5Ω
(2分)
得R1=4.5Ω
(2分)
所以金属杆单位长度的电阻 r= Ω/m=4.5Ω/m
(2分)
Ω/m=4.5Ω/m
(2分)
⑵有风时: U2=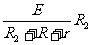 得R2=1.5Ω (2分)
得R2=1.5Ω (2分)
此时,弹簧长度L=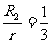 m (2分)
m (2分)
压缩量x=L0-L=(1-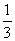 )m=
)m=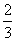 m
(1分)
m
(1分)
由平衡得此时风力:F=kx=120×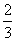 =80N (2分)
=80N (2分)
4.我国“神舟”六号宇宙已经发射成功,当时在飞船控制中心的大屏幕上出现的一幅卫星运行轨迹图,如图所示,它记录了“神舟”六号飞船在地球表面垂直投影的位置变化;图中表示在一段时间内飞船绕地球圆周飞行四圈,依次飞经中国和太平洋地区的四次轨迹①、②、③、④,图中分别标出了各地点的经纬度(如:在轨迹①通过赤道时的经度为西经156°,绕行一圈后轨迹②再次经过赤道时经度为180°……),若已知地球半径为R,地球表面处的重力加速度g,地球自转周期为24h,根据图中的信息:
⑴如果飞船运行周期用T表示,试写出飞船离地面高度的表达式
⑵飞船运行一周,地球转过的角度是多少?
 ⑶求飞船运行的周期
⑶求飞船运行的周期
解.①由万有引力提供向心力,即 ----------- 1分
----------- 1分
在地球表面处 mg =GMm/ R2----------- 1分
可求得飞船的轨道半径: -----------
2分
-----------
2分
②飞船每运行一周,地球自转角度为180°-156°= 24°----------- 2分
③神舟飞船运行的周期T为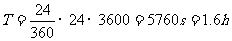 --------------3分
--------------3分
3.一个质量为m带电量为+q的小球以水平初速度v0自h高度做平抛运动.不计空气阻力.重力加速度为g.试回答下列问题
⑴若在空间竖直方向加一个匀强电场,发现小球水平抛出后做匀速直线运动,电场强度E是多大?
⑵撤消匀强电场后,小球再水平抛出至第一落地点P的过程,发生位移S的大小是多少?
⑶若在空间再加一个垂直纸面向外的匀强磁场,发现小球第一次落地仍然是P点.试问磁感应强度B是多大?
 解:(1)mg=qE
解:(1)mg=qE 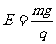 (2分)
(2分)
(2)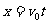 (1分)
(1分) 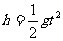 (1分)
(1分)
得到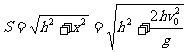 (1分)
(1分)
(3)R2=x2+(R-h)2 (1分) 得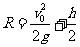 (1分)
(1分)
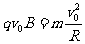
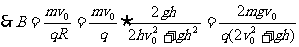 (2分)
(2分)
(此小题算对一种情况即给满分)
2.如图所示,半径R=0.5m的光滑圆弧面CDM分别与光滑斜面体ABC和斜面MN相切于 C、M点,O为圆弧圆心,D为圆弧最低点.斜面体ABC固定在地面上,顶端B安装一定滑轮,一轻质软细绳跨过定滑轮(不计滑轮摩擦)分别连接小物块P、Q (两边细绳分别与对应斜面平行),并保持P、Q两物块静止.若PC间距为L1=0.25m,斜面MN足够长,物块P质量m1=3kg,与MN间的动摩擦因数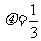 ,求:
,求:
(1)小物块Q的质量m2;
(2)烧断细绳后,物块P第一次到达D点时对轨道的压力大小;
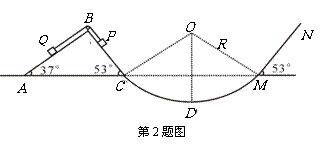 (3)P物块P第一次过M点后0.3s到达K点,则 MK间距多大;
(3)P物块P第一次过M点后0.3s到达K点,则 MK间距多大;
(4)物块P在MN斜面上滑行的总路程.
解.(17分)(1)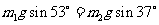 -------------------2分
-------------------2分
得:m2=4kg-------- ----1分
(2)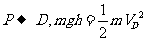 -------
------1分
-------
------1分
 ----
-------1分
----
-------1分
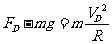 ------ -------1分
------ -------1分
得:FD=78N---- --------1分
由牛顿第三定律得,物块P对轨道的压力大小为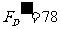 N ------------1分
N ------------1分
(3)PM段: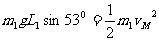 vM=2m/s------- --------1分
vM=2m/s------- --------1分
沿MN向上运动:a1=gsin530+μgcos530=10m/s2---- --------1分
vM= a1 t1 t1=0.2s---- --------1分
所以t1=0.2s时,P物到达斜面MN上最高点,故返回 -------1分
-------1分
沿MN向下运动:a2=gsin53_μgcos53 = 6m/s2 ----- ------1分
 m----- -------1分
m----- -------1分
(4)末状态为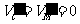
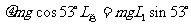 ----
--------2分
----
--------2分
得L总=1.0m----- -------1分
1. 如图所示的直角坐标系oxy中,C点坐标为(a,b).现有一带电量为q(q>0),质量为m的粒子,从O点以
如图所示的直角坐标系oxy中,C点坐标为(a,b).现有一带电量为q(q>0),质量为m的粒子,从O点以 速度沿负y轴方向发出,经过合适的“场”后到达C处(不计粒子重力).
速度沿负y轴方向发出,经过合适的“场”后到达C处(不计粒子重力).
(1)若在y≤0的空间存在垂直于纸面向内的匀强磁场,求该粒子从O到C经历的时间及对应的磁感应强度B.
(2)若仅在空间恰当的位置D处(D点图中未画出)放置一负点电荷,也能使该粒子从O点发出,速率不变地经过C点,求D点的坐标及该负点电荷的电量Q (已知静电力常量为K).
 解.(12分)(1)如图,粒子在磁场中,
解.(12分)(1)如图,粒子在磁场中,
R=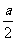 ---------------
--1分
---------------
--1分
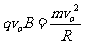 --------
-----2分
--------
-----2分
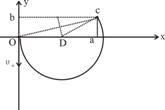 由①②得:
由①②得: ----
-----1分
----
-----1分
磁场中时间 -----
-----1分
-----
-----1分
无场区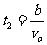 ------
------1分
------
------1分
O到C: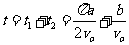 -----
---1分
-----
---1分
(2)如图,连接OC,作OC的中垂线交X轴即是D点。
设r=OD=CD。
则r2=b2+(a-r)2 ------- --- ---1分
得 ---------
---1分
---------
---1分
所以D坐标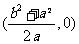 ---------- ---1分
---------- ---1分
由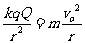 --------
-----1分
--------
-----1分
得Q= ------------1分
------------1分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com