
3.(2010年苏北四市调研)给出下列关于互不相同的直线m、l、n和平面α、β的四个命题:
①若m⊂α,l∩α=A,点A∉m, 则l与m不共面;
②若m、l是异面直线,l∥α,m∥α,且n⊥l,n⊥m,则n⊥α;
③若l∥α,m∥β,α∥β,则l∥m;
④若l⊂α,m⊂α,l∩m=A,l∥β,m∥β,则α∥β.
其中为真命题的是________.
解析:③中若l⊂β,m⊂α,α∥β⇒l∥m或l,m异面,所以②错误.而其它命题都正确.答案:①②④
2.已知m、n是不同的直线,α、β是不重合的平面,给出下列命题:
①若m∥α,则m平行于平面α内的无数条直线;
②若α∥β,m⊂α,n⊂β,则m∥n;
③若m⊥α,n⊥β,m∥n,则α∥β;
④若α∥β,m⊂α,则m∥β.
其中,真命题的序号是________.(写出所有真命题的序号)
解析:②中α∥β,m⊂α,n⊂β⇒m∥n或m,n异面,所以②错误.而其它命题都正确.答案:①③④
1.已知m、n是两条不同直线,α,β是两个不同平面,下列命题中的真命题是_.
①如果m⊂α,n⊂β,m∥n,那么α∥β
②如果m⊂α,n⊂β,α∥β,那么m∥n
③如果m⊂α,n⊂β,α∥β且m,n共面,那么m∥n
④如果m∥n,m⊥α,n⊥β,那么α⊥β
解析:m⊂α,n⊂β,α∥β⇒m,n没有公共点.又m,n共面,
所以m∥n.答案:③
6.在三棱锥 中,
中, 是边长为
是边长为 的正三角形,平面
的正三角形,平面 平面
平面 ,
, ,
,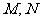 分别是
分别是 的中点.
的中点.
 (1)证明
(1)证明 ;(2)求二面角
;(2)求二面角 的大小;(3)求点
的大小;(3)求点 到平面
到平面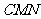 的距离.
的距离.
5. 在四棱锥
在四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱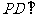 底面
底面 ,
,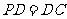 ,
, 是
是 中点,作
中点,作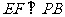 交
交 于
于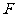 .
.
(1)证明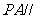 平面
平面 :
:
(2)证明 平面
平面 ;
;
(3)求二面角 的大小.
的大小.
4.平行六面体 的底面是矩形,侧棱长为
的底面是矩形,侧棱长为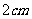 ,点
,点 在底面
在底面 上的射影
上的射影 是
是 的中点,
的中点,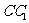 与底面
与底面 成
成 的角,二面角
的角,二面角 的平面角等于
的平面角等于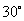 ,求此平行六面体的表面积.
,求此平行六面体的表面积.
3.已知正方形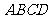 ,
,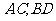 交于点
交于点 ,若将正方形沿
,若将正方形沿 折成
折成 的二面角,并给出四个结论:(1)
的二面角,并给出四个结论:(1)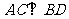 ;(2)
;(2)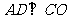 ;(3)
;(3) 为正三角形;(4)
为正三角形;(4) ,则其中正确命题的序号为
.
,则其中正确命题的序号为
.
2.已知正三棱锥两个相邻侧面所成二面角为 ,那么
,那么 的取值范围( )
的取值范围( )




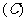


 或
或
1.过正方形 的顶点
的顶点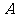 ,引
,引 ⊥平面
⊥平面 ,若
,若 ,则平面
,则平面 和平面
和平面 所成的二面角的大小是( )
所成的二面角的大小是( )

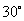


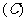


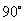
 例1.如图,点
例1.如图,点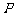 为斜三棱柱
为斜三棱柱 的侧棱
的侧棱 上一点,
上一点, 交
交 于点
于点 ,
,
 交
交 于点
于点 ,(1)求证:
,(1)求证: ;
;
(2)在任意 中有余弦定理:
中有余弦定理: . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
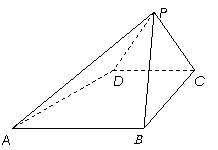 例2.如图,已知四棱锥
例2.如图,已知四棱锥 的底面是直角梯形,
的底面是直角梯形, ,
, ,侧面
,侧面 底面
底面 .
.
(1) 与
与 是否相互垂直,请证明你的结论;
是否相互垂直,请证明你的结论;
(2)求二面角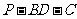 的大小;
的大小;
(3)求证:平面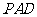 ⊥平面
⊥平面 .
.
解:(1) 与
与 相互垂直.证明如下:
相互垂直.证明如下:
取 的中点
的中点 ,连结
,连结 ,交
,交 于点
于点 ;连结
;连结 .
.
∵ ,∴
,∴ .又∵平面
.又∵平面 ⊥平面
⊥平面 ,
,
 平面
平面 ∩平面
∩平面 ,∴
,∴ ⊥平面
⊥平面 .
.
在梯形 中,可得
中,可得 ,
,
∴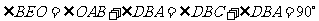 ,
,
即 , ∴
, ∴ .
.
(2)连结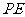 ,
,
由 ⊥平面
⊥平面 ,
, ,可得
,可得 ,
,
∴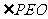 为二面角
为二面角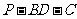 的平面角,
的平面角,
设 ,则在
,则在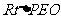 中,
中,
 ∴二面角
∴二面角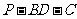 为
为 .
.
(3)取 的中点
的中点 ,连结
,连结 ,由题意知:平面
,由题意知:平面 ⊥平面
⊥平面 ,
,
则同“(1)”可得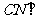 平面
平面 .
.
取 的中点
的中点 ,连结
,连结 ,则由
,则由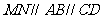 ,
,
 ,得四边形
,得四边形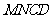 为平行四边形. ∴
为平行四边形. ∴ ,
,
∴ ⊥平面
⊥平面 .∴平面
.∴平面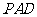 ⊥平面
⊥平面 .
.
解答二:
取 的中点
的中点 ,由侧面
,由侧面 ⊥底面
⊥底面 ,
,
 是等边三角形,
是等边三角形,
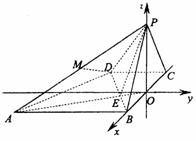 得
得 ⊥底面
⊥底面 .
.
以 为原点,以
为原点,以 所在直线为
所在直线为 轴,
轴,
过点 与
与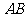 平行的直线为
平行的直线为 轴,
轴,
建立如图所示的空间直角坐标系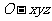 ,
,
设 ,则在直角梯形中,
,则在直角梯形中, ,
,
在等边三角形 中,
中,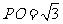 .
.
∴
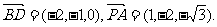
(1) 与
与 相互垂直.证明如下:
相互垂直.证明如下:
∵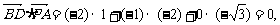
∴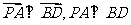 .
.
(2)连结 ,设
,设 与
与 相交于点
相交于点 ;连结
;连结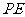 .
.
由 得
得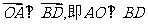 .
.
又∵ 为
为 在平面
在平面 内的射影,
内的射影,
∴ ,
,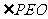 为二面角
为二面角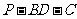 的平面角.
的平面角.
在 中,
中, .
.
 在
在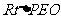 中,
中,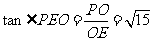 .
.
∴二面角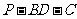 为
为 .
.
(3)取 的中点
的中点 ,连结
,连结 ,则
,则 的坐标为
的坐标为 .
.
又 ,
, ,
,
∴
 .
.
∴
∴ ⊥平面
⊥平面 . ∴平面
. ∴平面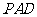 ⊥平面
⊥平面 .
.
小结:三垂线定理是求二面角的平面角的又一常用方法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com