
1.设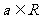 ,
,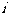 是虚数单位,则当
是虚数单位,则当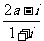 是纯虚数时,实数
是纯虚数时,实数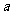 为 ( )
为 ( )
A. B.
B.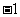 C.
C.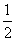 D.
D.
24.选修4-5:不等式证明选讲
已知函数
(1)求函数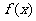 的值域;
的值域;
(2)若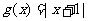 ,解不等式
,解不等式
23.选修4-4:坐标系与参数方程
已知曲线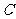 的极坐标方程为
的极坐标方程为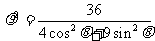 ,
,
(1)若以极点为原点,极轴所在的直线为 轴,求曲线
轴,求曲线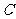 的直角坐标方程;
的直角坐标方程;
(2)若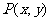 是曲线
是曲线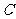 上的一个动点,求
上的一个动点,求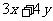 的最大值
的最大值
22.选修4-1:几何证明选讲
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.
 求证:(1)
求证:(1)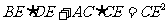 ;
;
(2)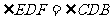 ;
;
(3)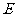 ,
,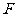 ,
,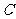 ,
,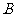 四点共圆
四点共圆
21.(本小题满分12分)
已知函数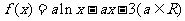
(1)当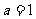 时,求函数
时,求函数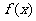 的单调区间;
的单调区间;
(2)若函数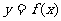 的图像在点
的图像在点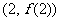 处的切线的倾斜角为
处的切线的倾斜角为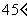 ,问:
,问: 在什么范围取值时,函数
在什么范围取值时,函数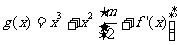 在区间
在区间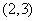 上总存在极值?
上总存在极值?
(3)当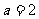 时,设函数
时,设函数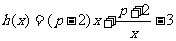 ,若对任意地
,若对任意地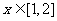 ,
,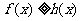 恒成立,求实数
恒成立,求实数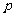 的取值范围
的取值范围
选答题(请考生在第22、23、24三道题中任选一题做答,并用2B铅笔在答题卡上把所选题目的题号涂黑注意所做题号必须与所涂题目的题号一致,并在答题卡指定区域答题如果多做,则按所做的第一题计分)
20.(本小题满分12分)
已知椭圆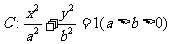 的离心率为
的离心率为 ,过焦点且垂直于长轴的直线被椭圆截得的弦长为
,过焦点且垂直于长轴的直线被椭圆截得的弦长为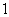 ,过点
,过点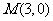 的直线与椭圆
的直线与椭圆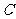 相交于两点
相交于两点 ,
,
(1)求椭圆的方程;
(2)设 为椭圆上一点,且满足
为椭圆上一点,且满足 (
( 为坐标原点),当
为坐标原点),当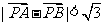 时,求实数
时,求实数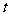 的取值范围
的取值范围
19.(本小题满分12分)
如图,四棱锥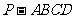 中,侧面
中,侧面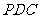 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面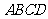 是
是 的菱形,
的菱形, 为
为 的中点
的中点
(1)求证: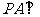 平面
平面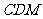 ;
;
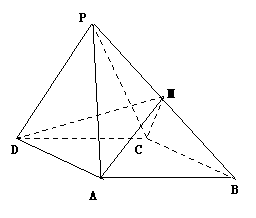 (2)点
(2)点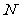 在棱
在棱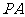 上,且
上,且 ,求四面体
,求四面体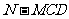 的体积
的体积
18.(本小题满分12分)
哈尔滨市第九中学高三某班有女同学45名,男同学15名,老师按照分层抽样的方法组建一个4人的课外兴趣小组
(1)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(2)经过一个月的学习讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出1名同学做实验,该同学做完后,再从小组内剩下的同学中选1名同学做实验,求选出的两名同学中恰好有一名男同学的概率;
(3)实验结束后,第一次做实验的同学得到的实验数据为68、70、71、72、74,第二次做实验的同学得到的实验数据时69、70、70、72、74,请问哪位同学的实验更稳定?并说明理由
17.(本小题满分12分)
已知函数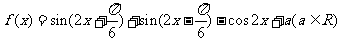
(1)求函数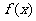 的最小正周期和图像的对称轴方程;
的最小正周期和图像的对称轴方程;
(2)若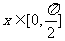 时,
时,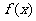 的最小值为
的最小值为 ,求
,求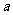 的值
的值
16.给出以下四个结论:
(1)函数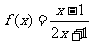 的对称中心是
的对称中心是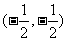 ;
;
(2)若关于 的方程
的方程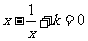 在
在 没有实数根,则
没有实数根,则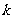 的取值范围是
的取值范围是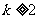 ;
;
(3)已知点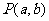 与点
与点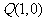 在直线
在直线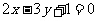 两侧,当
两侧,当 且
且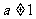 ,
, 时,
时,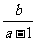 的取值范围为
的取值范围为 ;
;
(4)若将函数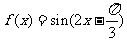 的图像向右平移
的图像向右平移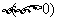 个单位后变为偶函数,则
个单位后变为偶函数,则 的最小值是
的最小值是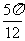 ;
;
其中正确的结论是:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com