
20.(本小题满分10分)
解: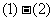 得,
得,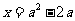 --------2分
--------2分
∴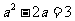 ,
,
解得 ---------4分
---------4分
将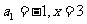 代入(2)得
代入(2)得
 ,
,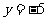 ,即
,即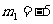 ,
---------6分
,
---------6分
将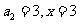 代入(2)得
代入(2)得


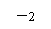


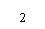

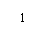
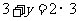 ,
, ,即
,即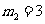 --------8分
--------8分
∴
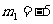
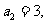
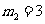 --------10分
--------10分
19.(本小题满分10分)
证明:∵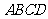 是等腰梯形
是等腰梯形
∴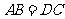 ,
--------2分
,
--------2分
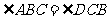 --------4分
--------4分
∵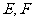 分别为
分别为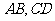 的中点
的中点
∴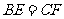 --------6分
--------6分
∴ --------8分
--------8分
∴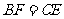 --------10分
--------10分
18.(本小题满分9分)
解:(1) ∵ --------2分
--------2分
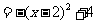 --------4分
--------4分
∴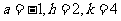 --------7分
--------7分
(2)函数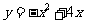 图像的顶点坐标为
图像的顶点坐标为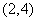 ,--------8分
,--------8分
对称轴方程为 --------9分
--------9分
17.(本小题满分9分)
先化简,后计算: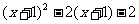 ,其中
,其中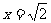
解法1: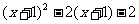
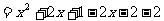 ---------4分
---------4分
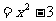 --------6分
--------6分
将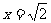 得,
得,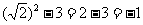 --------9分
--------9分
(其它解法酌情评分)
解法2: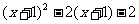

将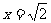 得,
得,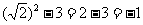
解法3: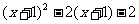

将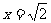 得,
得,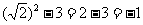
解法4: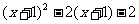
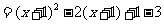
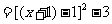
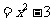
将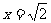 得,
得,
14.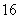 15.
15.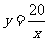 16.7,16(第一空2分,第二空1分)
16.7,16(第一空2分,第二空1分)
1. 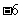 12.
12.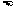 13.
13.
25. (本小题满分14分)
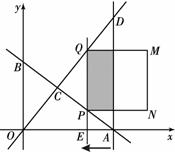 如图12,直线
如图12,直线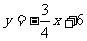 分别与x轴、y轴交于A、B两点;直线
分别与x轴、y轴交于A、B两点;直线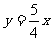 与
与 交于点
交于点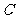 ,与过点
,与过点 且平行于
且平行于 轴的直线交于点
轴的直线交于点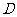 .
.
点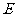 从点
从点 出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿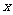 轴向
轴向
左运动.过点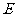 作
作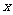 轴的垂线,分别交直线
轴的垂线,分别交直线 、
、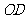
于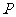 、
、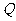 两点,以
两点,以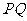 为边向右作正方形
为边向右作正方形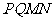 .设
.设
正方形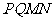 与△
与△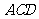 重叠部分(阴影部分)的面
重叠部分(阴影部分)的面
积为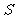 (平方单位),点
(平方单位),点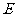 的运动时间为
的运动时间为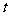 (秒).
(秒).
(1)求点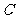 的坐标.
的坐标.
(2)当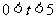 时,求
时,求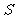 与
与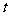 之间的函数关系式.
之间的函数关系式.
|
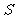 的最大值.(2分)
的最大值.(2分)
(4)当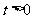 时,直接写出点
时,直接写出点 在正方形
在正方形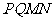 内部时
内部时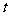 的取值范围.
的取值范围.
2010年初中毕业班综合测试
数学答案及评分标准
24.(本小题满分14分)
青海省玉树县发生强烈地震,某工厂计划连夜为灾区生产
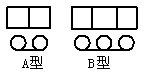
 两种特殊型号的学生桌椅(如右图)
两种特殊型号的学生桌椅(如右图)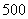 套,以解决
套,以解决
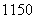 名学生的学习问题,一套
名学生的学习问题,一套 型桌椅(一桌两椅)需木
型桌椅(一桌两椅)需木
料 ,一套
,一套 型桌椅(一桌三椅)需木料
型桌椅(一桌三椅)需木料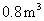 ,工
,工
厂现有库存木料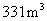 .
.
(1)求生产 两种型号的学生桌椅有多少种生产方案?
两种型号的学生桌椅有多少种生产方案?
(2)现要把生产的全部桌椅尽快运往地震灾区,已知每套 型桌椅的生产成本为60元,运费2元;每套
型桌椅的生产成本为60元,运费2元;每套 型桌椅的生产成本为80元,运费4元,求总费用
型桌椅的生产成本为80元,运费4元,求总费用 (元)与生产
(元)与生产 型桌椅
型桌椅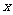 (套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用
(套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用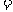 生产成本
生产成本 运费)
运费)
(3)按照(2)的方案计算,还有没有剩余木料?如果有,请直接写出用剩余木料再生产以上两种型号的桌椅,最多还可以为多少名学生提供桌椅;如果没有,请说明理由.
23. (本小题满分12分)
(本小题满分12分)
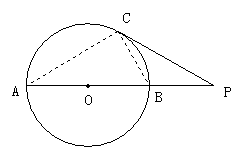
如图11,点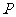 在⊙O的直径
在⊙O的直径 的延长线上,
的延长线上,
|
 切⊙O于点
切⊙O于点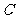 ,
, ,连结
,连结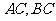 .
.
(1)求证: .
.
(2)若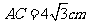 ,求⊙O的半径
,求⊙O的半径 .
.
|
22. (本小题满分12分)
(本小题满分12分)
如图10,A, B两点分别在x轴, y轴的正半轴上,
且OA=4, OB=2
(1)写出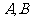 点的坐标,并求线段
点的坐标,并求线段 的长度;
的长度;
(2)用直尺和圆规作一条直线l,把△ABC分割成两个
等腰三角形(作图不要求写作法,但须保留作图痕迹);
(3)任意选取其中一个等腰三角形,用直尺和圆规作出这个
|
但须保留作图痕迹).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com