10．如图，在三棱锥S－ABC中，OA＝OB，O为BC中点，SO⊥平面ABC，E为SC中点，F为AB中点．

(1)求证：OE∥平面SAB；

(2)求证：平面SOF⊥平面SAB.

证明：(1)取AC的中点G，连结OG，EG，

∵OG∥AB，EG∥AS，EG∩OG＝G，SA∩AB＝A，

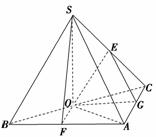∴平面EGO∥平面SAB，OE⊂平面OEG

∴OE∥平面SAB

(2)∵SO⊥平面ABC，

∴SO⊥OB，SO⊥OA，

又∵OA＝OB，SA²＝SO²+OA²，SB²＝SO²+OB²，

∴SA＝SB，又F为AB中点，

∴SF⊥AB，∵SO⊥AB，

∵SF∩SO＝S，∴AB⊥平面SOF，

∵AB⊂平面SAB，∴平面SOF⊥平面SAB.

9．在正四棱锥P－ABCD中，PA＝AB，M是BC的中点，G是△PAD的重心，则在平面PAD中经过G点且与直线PM垂直的直线有________条．

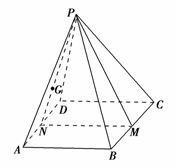解析：设正四棱锥的底面边长为a，则侧棱长为a.

由PM⊥BC，

∴PM＝＝a，

连结PG并延长与AD相交于N点，

则PN＝a，MN＝AB＝a，

∴PM²+PN²＝MN²，

∴PM⊥PN，又PM⊥AD，

∴PM⊥面PAD，

∴在平面PAD中经过G点的任意一条直线都与PM垂直．答案：无数

8．(2010年江苏昆山模拟)在矩形ABCD中，AB＝3，AD＝4，P在AD上运动，设∠ABP＝θ，将△ABP沿BP折起，使得平面ABP垂直于平面BPDC，AC长最小时θ的值为________．

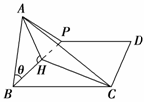解析：过A作AH⊥BP于H，连CH，∴AH⊥平面BCDP.

∴在Rt△ABH中，AH＝3sinθ，BH＝3cosθ.

在△BHC中，CH²＝(3cosθ)²+4²－2×4×3cosθ×cos(90°－θ)，

∴在Rt△ACH中，

AC²＝25－12sin2θ，

∴θ＝45°时，AC长最小．答案：45°

7．如图所示，在斜三棱柱ABC－A₁B₁C₁中，∠BAC＝90°，BC₁⊥AC，则C₁在底面ABC上的射影H必在直线______上．

解析：由AC⊥AB，AC⊥BC₁，AC⊥平面ABC₁，AC⊂平面ABC，∴平面ABC₁⊥平面ABC，C₁在平面ABC上的射影H必在两平面的交线AB上．答案：AB

6．已知二面角α－l－β的大小为30°，m、n为异面直线，m⊥平面α，n⊥平面β，则m、n所成的角为________．

解析：∵m⊥α，n⊥β，

∴m、n所成的夹角与二面角α－l－β所成的角相等或互补．

∵二面角α－l－β为30°，

∴异面直线m、n所成的角为30°.答案：30°

5．设a，b，c表示三条直线，α，β表示两个平面，则下列命题的逆命题不成立的是________．

①c⊥α，若c⊥β，则α∥β

②b⊂β，c是a在β内的射影，若b⊥c，则a⊥b

③b⊂β，若b⊥α，则β⊥α

④b⊂α，c⊄α，若c∥α，则b∥c

解析：当b⊂β，若β⊥α，则未必有b⊥α.答案：③

4．已知两条不同的直线m，n，两个不同的平面α，β，则下列命题中正确的是_．

①若m⊥α，n⊥β，α⊥β，则m⊥n

②若m⊥α，n∥β，α⊥β，则m⊥n

③若m∥α，n∥β，α∥β，则m∥n

④若m∥α，n⊥β，α⊥β，则m∥n

解析：易知①正确．而②中α⊥β且m⊥α⇒m∥β或m∈β，又n∥β，容易知道m，n的位置关系不定，因此②错误．而③中分别平行于两平行平面的直线的位置关系不定，因此③错误．而④中因为②不对，此项也不对．综上可知①正确．答案：①

3．设m，n是两条不同的直线， α，β是两个不同的平面，则下列命题正确的是．

①m⊥α，n⊂β，m⊥n⇒α⊥β　 ②α∥β，m⊥α，n∥β ⇒m⊥n

③α⊥β，m⊥α，n∥β ⇒m⊥n　 ④α⊥β，α∩β＝m，n⊥m⇒n⊥β

解析：①错，不符合面面垂直的判断定理的条件；②由空间想象易知命题正确；③错，两直线可平行；④错，由面面垂直的性质定理可知只有当直线n在平面α内时命题才成立．答案：②

2．设α，β为不重合的平面，m，n为不重合的直线，则下列命题正确的是________．

①若m⊂α，n⊂β，m∥n，则α∥β

②若n⊥α，n⊥β，m⊥β，则m⊥α

③若m∥α，n∥β，m⊥n，则α⊥β

④若α⊥β，α∩β＝n，m⊥n，则m⊥α

解析：由n⊥α，n⊥β可得α∥β，又因m⊥β，所以m⊥α.答案：②

1．设a，b是两条不同的直线，α，β是两个不同的平面，则能得出a⊥b的是____．

①a⊥α，b∥β，α⊥β　 ②a⊥α，b⊥β，α∥β

③a⊂α，b⊥β，α∥β　 ④a⊂α，b∥β，α⊥β

解析：由α∥β，b⊥β ⇒b⊥α，又a⊂α，故a⊥b.答案：③