8.经过悠长历史的演变，中华文化不但在中国大陆广袤的土地上根深蒂固，而且在海外有华人的地方就有中华文化，中华儿女不管到哪里，不仅能保留自己的习俗文化，还能融入到当地的民情风俗里。这有利于

1吸收、借鉴其他民族文化中的积极成分　　 2各种文化在和睦中的关系中交流　 3增强对自身文化的认同、对外域文化的理解　　 4中华文化通过和平方式取代海外当地文化

A.1234　　　　　 B.124　　　　　 C.123　　　　　　 D.134

7.下列属于上题结论的重要原因的是

A.中华文化的包容性　　　　　　　　 B.华人固守传统观念

C.中国人口众多　　　　　　　　　　 D.华人在海外的影响力强

儒学作为宝贵文化遗产辐射中华民族两千多年，在两岸文化发展史上占有重要地位。历史上传统儒学曾经辐射东亚和南亚形成特有的儒家文化圈，今天儒学精华随着中国在50多个国家200所孔子文化学院的建立重新走向世界，对世界文化产生积极影响。据此回答8—9题：

6.传统的儒家思想在两岸人民的心中根深蒂固，从一个侧面反映了中华文化

A.博大精深　　　　　　　　　　　　 B.源远流长

C.一枝独秀　　　　　　　　　　　　 D.有着辉煌的历程

5.当今世界，文化的交流和传播日渐成为各国交往的重要内容，文化的矛盾冲突也日渐成为国际竞争和国际冲突的一个重要方面。这表明

A.意识形态的差异是国家间冲突的根源

B.国际竞争的实质是以文化为核心的综合国力的较量

C.文化在综合国力中已成为决定性因素

D.文化的力量已成为一个国家综合国力的重要组成部分

儒学与两岸文化发展密不可分，是两岸文化的重要根基。在海峡两岸的人民心中儒家思想早已根深蒂固。据此回答6—7题：

4.材料说明

A.古时的尊敬师长观念已过时

B.取其精华、去其糟粕，推陈出新、革故鼎新，这是文化创新必然要经历的过程

C.现代的尊敬师长观念已完全与传统的尊敬师长观念不同

D.博采众长，才能实现文化创新

3.孔子的哲学强调阴阳互补、和谐与永恒变易以及天人合一的宇宙观，是中国古典哲学的重要基础。孔子的宇宙观包含着丰富的

A.唯物主义思想　　　　　　　　　　　 B.唯心主义思想

C.辩证法思想　　　　　　　　 　　　　D.形而上学思想

中华文化源远流长，中国自古就是礼仪之邦，古时尊敬师长是人们遵守的纲常之一，现在仍然谈尊敬师长，却已赋予了新的时代内涵。师生关系再也不是“一日为师，终身为父”的师徒观，而是指导、帮助、朋友般的教学相长关系。据此回答4—5题：

2.我们要发掘和丰富孔子儒家思想文化博大精深的思想内涵，使之不断创新发展，以“和而不同”、“兼收并蓄”的胸怀走向世界。“和而不同”指的是

A.中华文化能和其他民族的文化和谐相处

B.中华文化能在文化交往中吸取、借鉴其他民族文化中的积极成分

C.中华文化和其他民族文化虽不同但在逐渐走向融合

D.中华文化和别的民族文化是互不联系的

1.孔子的主要言行，经其弟子和再传弟子的收集整理编成《论语》一书，这本成为儒家学派的经典。这主要说明

A.中华文化源远流长

B.中华文化博大精深

C.史书典籍是中华文化一脉相传的重要见证

D.儒家文化、儒家思想成为中华文化的缩影

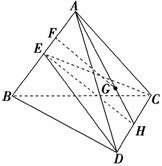
12．(2010年江苏淮安模拟)如图，已知空间四边形ABCD中，BC＝AC，AD＝BD，E是AB的中点．

求证：(1)AB⊥平面CDE；

(2)平面CDE⊥平面ABC；

(3)若G为△ADC的重心，试在线段AE上确定一点F，使得GF∥平面CDE.

证明：(1)⇒CE⊥AB，同理，

⇒DE⊥AB，

又∵CE∩DE＝E，∴AB⊥平面CDE.

(2)由(1)知AB⊥平面CDE，

又∵AB⊂平面ABC，

∴平面CDE⊥平面ABC.

(3)连结AG并延长交CD于H，连结EH，则＝，

在AE上取点F使得＝，

则GF∥EH，

11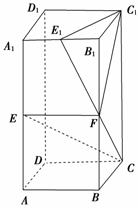．在长方体ABCD－A₁B₁C₁D₁中，AA₁＝2AB＝2BC，E，F，E₁分别是棱AA₁，BB₁，A₁B₁的中点．

(1)求证：CE∥平面C₁E₁F；

(2)求证：平面C₁E₁F⊥平面CEF.

证明：(1)取CC₁的中点G，连结B₁G交C₁F于点F₁，连结E₁F₁，A₁G，FG，

∵F是BB₁的中点，BCC₁B₁是矩形，

∵四边形FGC₁B₁也是矩形，

∴FC₁与B₁G相互平分，即F₁是B₁G的中点．

又E₁是A₁B₁的中点，∴A₁G∥E₁F₁.

又在长方体中，AA₁綊CC₁，E，G分别为AA₁，CC₁的中点，

∴A₁E綊CG，∴四边形A₁ECG是平行四边形，

∴A₁G∥CE，∴E₁F₁∥CE.

∵CE⊄平面C₁E₁F，E₁F₁⊂平面C₁E₁F，

∴CE∥平面C₁E₁F.

(2)∵长方形BCC₁B₁中，BB₁＝2BC，F是BB₁的中点，

∴△BCF、△B₁C₁F都是等腰直角三角形，

∴∠BFC＝∠B₁FC₁＝45°，

∴∠CFC₁＝180°－45°－45°＝90°，

∴C₁F⊥CF.

∵E，F分别是矩形ABB₁A₁的边AA₁，BB₁的中点，

∴EF∥AB.

又AB⊥平面BCC₁B₁，又C₁F⊂平面BCC₁B₁，

∴AB⊥C₁F，∴EF⊥C₁F.

又CF∩EF＝F，∴C₁F⊥平面CEF.

∵C₁F⊂平面C₁E₁F，∴平面C₁E₁F⊥平面CEF.