
20.(本小题满分12分)
如图,在正四棱锥S-ABCD中,AB=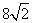 ,SA=10,M、N、O分别是SA、SB、BD的中点。
,SA=10,M、N、O分别是SA、SB、BD的中点。
(1)设P是OC的中点,证明:PN//平面BMD;
(2)求直线SO与平面BMD所成角的大小;
(3)在△ABC内是否存在一点G,使NG⊥平面BMD,若存在,求线段NG的长度;若不存在,说明理由。

19.(本小题满分12分)
已知函数 、
、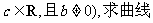
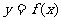 上斜率为c的切线与该曲线的公共点.
上斜率为c的切线与该曲线的公共点.
18.(本小题满分12分)
甲袋中装有若干质地、大小相同的黑球、白球,乙袋中装有若干个质地、大小相同的黑球、红球。某人有放回地从两袋中每次取一球,甲袋中每取到一黑球得2分,乙袋中每取到一黑球得1分,取得其它球得零分,规定他最多取3次,如果前两次得分之和超过2分即停止取球,否则取第三次,取球方式:先在甲袋中取一球,以后均在乙袋中取球,此人在乙袋中取到一个黑球的概率为0.8,用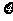 表示他取球结束后的总分,已知
表示他取球结束后的总分,已知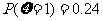
(1)求随机变量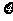 的数学期望;
的数学期望;
(2)试比较此人选择每次都在乙袋中取球得分超过1分与选择上述方式取球得分超过1 分的概率的大小.
17.(本小题满分12分)
已知A、B、C是△ABC三内角,向量
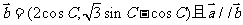
(1)求角A的大小;
(2)若AB+AC=4,求△ABC外接圆面积的取值范围。
16.已知抛物线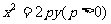 的焦点为F,过焦点F的直线交抛物线于A、B两点,分别过A、B作y轴的平行线依次交抛物线的准线于A1,B1两点,Q是A1B1的中点,连AQ、BQ、FA1,有下列命题:
的焦点为F,过焦点F的直线交抛物线于A、B两点,分别过A、B作y轴的平行线依次交抛物线的准线于A1,B1两点,Q是A1B1的中点,连AQ、BQ、FA1,有下列命题:
①△AA1F的垂心有可能在此抛物线 ;
②△AQB的外心有可能在此抛物线上;
③AQ、FA1、x轴相交于一点;
④过A、B两点的抛物线的两条切线的交点在此抛物线的准线上
上述命题正确的有 (写出所有真命题的序号)
15.一幅扑克牌除去大、小王共52张,洗好后,四个人顺次每人抓13张,则两个红A(即红桃A、方块A)在同一个人手中的概率为 。
14.已知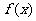 为定义在R上的增函数,且不等式
为定义在R上的增函数,且不等式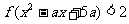 的解集为
的解集为
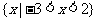 ,则实数a= 。
,则实数a= 。
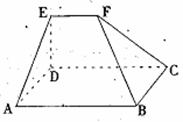
13.如图所示的几何体中,底面ABCD是矩形,AB=9,
BC=6,EF//平面ABCD,EF=3,△ADE和△BCF
都是正三角形,则几何体EFABCD的体积为
。
12.圆C1的方程为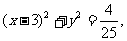 圆C2的方程
圆C2的方程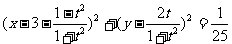
 过C2上任意一点作圆C1的两条切线PM、PN,切点分别为M、N,设PM与PN夹角的最大值为
过C2上任意一点作圆C1的两条切线PM、PN,切点分别为M、N,设PM与PN夹角的最大值为 ,则 ( )
,则 ( )
A.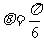 B.
B.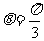 C.
C.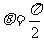 D.
D. 的取值有关
的取值有关
第Ⅱ卷
 二、填空题(本大题共4小题,每小题4分,共计16分,请把答案填在答题卡上)
二、填空题(本大题共4小题,每小题4分,共计16分,请把答案填在答题卡上)
11.设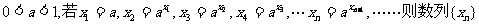 ( )
( )
A.递增 B.偶数项增,奇数项减
C.递减 D.奇数项增,偶数项减
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com