

5.正四面体ABCD的外接球球心为O,E为BC的中点,则二面A-BO-E的大小为( )
A. B.
B.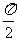 C.
C.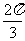 D.
D.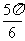
4.设D为△ABC的边AB上一点,P为△ABC内一点,且满足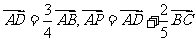 ,则
,则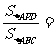 ( )
( )
A.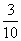 B.
B.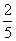 C.
C.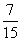 D.
D.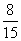
3.若 的取值范围是 ( )
的取值范围是 ( )
A.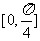 B.
B.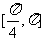 C.
C.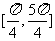 D.
D.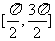
2.已知复数 是实数,则实数a等于 ( )
是实数,则实数a等于 ( )
A.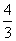 B.
B.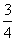 C.-
C.-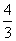 D.-
D.-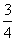
1.数值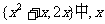 的取值范围是 ( )
的取值范围是 ( )
A. B.
B.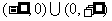
C.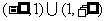 D.
D.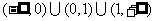
22.(本小题满分14分)
已知椭圆C: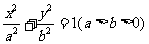 的一条准线方程为
的一条准线方程为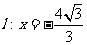 ,且左焦点F到l的距离为
,且左焦点F到l的距离为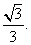
(1)求椭圆C的方程;
(2)已知斜率为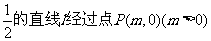 并与椭圆C交于不同的两点A、B,若对于椭圆C上任意一点M,都存在
并与椭圆C交于不同的两点A、B,若对于椭圆C上任意一点M,都存在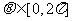 ,使得
,使得
 成立,求实数m的值.
成立,求实数m的值.
21.(本小题满分12分)
设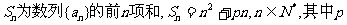 是实数。
是实数。
(1)求数列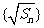 成等差数列的充要条件;
成等差数列的充要条件;
(2)若对于任意的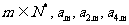 成等比数列,求p的值。
成等比数列,求p的值。
20.(本小题满分12分)
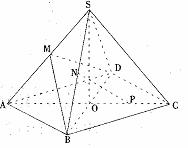
如图,在正四棱锥S-ABCD中,AB=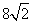 ,SA=10,M、N、O分别是SA、SB、BD的中点。
,SA=10,M、N、O分别是SA、SB、BD的中点。
(1)设P是OC的中点,证明:PN//平面BMD;
(2)在线段OA上是否存在一点Q,使得SQ⊥平面BMD,若存在,求线段SQ的长度;若不存在;说明理由。
19.(本小题满分12分)
已知函数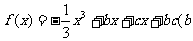 、
、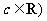 在
在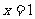 处有极值
处有极值 ,试确定b,c的值并求函数的递增区间.
,试确定b,c的值并求函数的递增区间.
18.(本小题满分12分)
甲袋中装有若干质地、大小相同的黑球、白球,乙袋中装有若干个质地、大小相同的黑球、红球。某人有放回地从两袋中每次取一球,甲袋中每取到一黑球得2分,乙袋中每取到一黑球得1分,取得其它球得零分,规定他最多取3次,如果前两次得分之和超过2分即停止取球,否则取第三次,取球方式:先在甲袋中取一球,以后均在乙袋中取球,此人在甲袋中取到一个黑球的概率为q,在乙袋中取到一个黑球的概率为0.8,用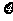 表示他取球结束后的总分,已知
表示他取球结束后的总分,已知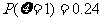
(1)求q的值;
(2)试比较此人选择每次都在乙袋中取球得分超过1分与选择上述方式取球得分超过1 分的概率的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com