
39.(22分)团结就是办量,力量源自热爱。2009年,无疑是新中国历史上值得铭记的一年,在这一年里,围绕新中国成立60周年,各地各部门都深入开展了群众性的爱国主义教育活动,极大的激发了人们的爱国热情,凝聚了人民力量,振奋了民族精神:由20 万军民参加的60年国庆庆典系列活动,激发了亿万群众浓浓的爱国心,家国情和民族自豪感,自信心;具有广泛群众参与度的“双百”人物(100位为新中国成立做出突出贡献的英雄模范人物和100位新中国成立以来感动中国的人物)和道德模范评选活动中,每一张选票都表达了对英雄模范的崇敬,都凝聚着对人生价值的思考,都寄托着对伟大祖国的美好祝福;春节、元宵节--辞旧迎新、幸福平安、家国兴旺;清明节--纪念先人、缅怀英烈;端午节--热爱祖国、求索创新、人与自然和谐共处;中秋节--团团圆圆、喜庆丰收;重阳节--尊老敬老、孝亲爱老……一个个传统节庆活动,成为中华民族认同标志和联结民族情感的纽带。
(1)60年一甲子,60年旧貌换新颜。新中国谱写了中华民族发展史上的壮丽篇章,庆祝新中国60华诞是全国各族人民政治生活中的一件大事、喜事、盛事。作为中国公民,你有何感触?(6分)
(2)结合上述材料,运用文化生活知识分析说明为什么要开展群众性的爱国主义教育活动?(10分)
(3)伟大的时代孕育伟大的精神。“双百”人物身上所承载的“忠于祖国、热爱人民、追求真理、坚持理想、艰苦奋斗、敢于胜衬、锐意进取、开拓创新、淡泊名利、无私奉献”的崇高精神对你实现人生价值有何启示?(6分)
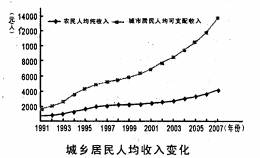
38.(30分)社会公平正义是社会和谐的基本条件,制度是社会公平正义的根本保证。从中央经济工作会议到今年“两会”,深化收入分配体制改革成为社会关注的热点。某校高三(2)班学生就“我国的收入分配体制改革”为课题开展探究学习,现在请你参与其中。
分配之变:
改革开放以来我国收入分配制度的探索
|
十一届三中全会 |
十二大 |
十三大 |
十四大 |
十五大 |
十六大 |
十七大 |
|
提出了“克服平均主义”,以农村为突破口,推行了家庭联产承包责任制,这是分配制度的重大改革。 |
提出深化分配制度改革,进一步贯彻落实按劳分配的社会主义原则。 |
指出社会主义初级阶段的分配方式不可能是单一的,必须实行以按劳分配为主体的多种分配方式和正确的分配政策。 |
提出个人收入分配要坚持以按劳分配为主体、多种分配方式并存的制度。要“体现效率优先、兼顾公平 的原则”。 |
提出要把按劳分配和按生产要素分配结合起来。 |
提出要坚持按劳分配为主体、多种分配方式并存的分配制度,加强收入分配宏观调节,在经济发展的基础上。更加注重社会公平。 |
强调,要逐提高“两个”比重;初次分配和再分配都要处理好效率和公平的关系,再分配更加注重公平。 |
(1)联系上述信息,指出我国调整完善分配制度的经济原因,并结合唯物辩证法关于创新意识和社会进步的知识分析我国分配制度变革的意义。(9分)
分配之忧:
 三大收入在GDP分配中的比重
三大收入在GDP分配中的比重
|
|
劳动报酬 |
企业营业盈余 |
政府收入 |
|
1997年 |
53.5% |
21.23%. |
10.95% |
|
2007年 |
39.7% |
31.29% |
20.57% |
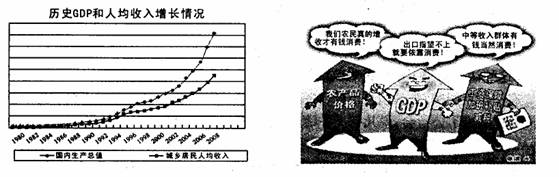
(2)以上图表反映了我国当前经济领域存在什么问题?请你运用所学经济生活知识谈谈应该怎样认识和解决这些问题?(13分)
分配之责:2010年2月27日,温家宝总理与网民交流时说:如果说把做大社会财富这个“蛋糕’’看作是政府的责任,那么,分好财富这个“蛋糕”,就是政府的良知。
(3)请你从政治生活角度,说说政府为什么要把社会财富这个“蛋糕”做大、分好?(8分)
37.(16分)我国于2009年1月27日建立了南极昆仑站。磁点指的67°00′S、140°00′E的地方。读图,回答下列问题.
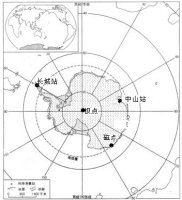
(1)下列说法完全正确的组合是: ( )
①南极洲是世界上平均海拔最低的大洲
②南极洲是世界上的淡水宝库
③长城站比中山站距祖国首都更近
④磁点位于中山站的东北方(4分)
A.①② B.③④
C.②④ D.①③
(2)南极大部分地方覆盖着很厚的冰层,却被称为"白色沙漠",为什么?(4分)
(3)与北极比南极为什么更冷?(4分)
(4)南极地区有着丰富的资源,对南极资源的开发和利用,你认为怎么做比较正确?(4分)
36.(30分)青藏高原(北纬25°-40°,东经74°-104°)是世界上最高的高原,平均海拔高度在4000米以上,有"世界屋脊"和"世界第三极"之称.回答下列问题.
(1)青藏高原是这样形成的?(4分)
(2)简述太阳能的特点;简析青藏地区太阳能丰富的原因。(10分)
(3)青藏高原为什么被称为"亚洲水塔"?(4分)
(4)简要说明青藏地区的河谷农业主要分布地区、主要农作物及分布原因。(12分)
21.(本小题满分14分)
已知函数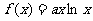 图像上点
图像上点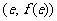 处的切线方程与直线
处的切线方程与直线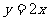 平行(其中
平行(其中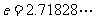 ),
),
(I)求函数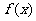 的解析式;
的解析式;
(II)求函数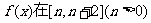 上的最小值;
上的最小值;
(III)对一切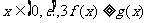 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
20.(本小题满分13分)
已知三点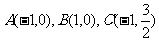 ,曲线E过C点,且动点P在曲线E上运动,并保持|PA|+|PB|的值不变.
,曲线E过C点,且动点P在曲线E上运动,并保持|PA|+|PB|的值不变.
(I)求曲线E的方程;
(II)若C、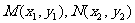 是曲线E上的不同三点,直线CM、CN的倾斜角互补.问直线MN的斜率是否是定值?如果是,求出该定值,如果不是,说明理由.
是曲线E上的不同三点,直线CM、CN的倾斜角互补.问直线MN的斜率是否是定值?如果是,求出该定值,如果不是,说明理由.
19.(本小题满分12分)
已知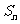 为数列
为数列 的前n项和,且
的前n项和,且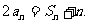
(I)若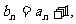 证明:数列
证明:数列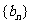 是等比数列;
是等比数列;
(II)求数列 的前n项和
的前n项和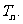
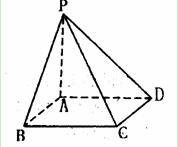
18.(本小题满分12分)
已知四棱锥P-ABCD的侧棱PA⊥平面ABCD,底面ABCD为正方形,且AB=AP=a.
(I)若E、F分别是PA、BC的中点,证明EF//平面PCD;
(II)求点A到平面PBD的距离.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com