12.(2010·湖南师大附中高三5月考试卷)在图中实线框所示的区域内同时存在着匀强磁场和匀强电场．一个带电粒子(不计重力)恰好能沿直线MN从左至右通过这一区域．那么匀强磁场和匀强电场的方向可能为下列哪种情况 (　　 )　　

A．匀强磁场方向竖直向上，匀强电场方向垂直于纸面向外

B．匀强磁场方向竖直向上，匀强电场方向垂直于纸面向里　　

C．匀强磁场方向垂直于纸面向里，匀强电场方向竖直向上

D．匀强磁场和匀强电场的方向都水平向右

[答案]BD

[解析]恰好能沿直线MN从左至右通过这一区域表明洛伦兹力与电场力平衡，假设粒子带正电，根据左手定则，若匀强磁场方向竖直向上，洛伦兹力直于纸面向外，电场力垂直于纸面向里时二力平衡，假设粒子带负电，洛伦兹力、电场力仍平衡，C正确；同理D正确.

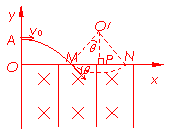
11.(2010·山东省费县一中高三调研测试)如图所示，直角坐标系xOy位于竖直平面内，在水平的x轴下方存在匀强磁场和匀强电场，磁场的磁感应为B,方向垂直xOy平面向里，电场线平行于y轴。一质量为m、电荷量为q的带正电的小球，从y轴上的A点水平向右抛出，经x轴上的M点进入电场和磁场，恰能做匀速圆周运动，从x轴上的N点第一次离开电场和磁场，MN之间的距离为L，小球过M点时的速度方向与x轴的方向夹角为。不计空气阻力，重力加速度为g，求

(1) 电场强度E的大小和方向；

(2) 小球从A点抛出时初速度v0的大小；

(3) A点到x轴的高度h.

[解析]⑴小球在电场、磁场中恰能做匀速圆周运动，说明电场力和重力平衡(恒力不能充当圆周运动的向心力)，有

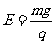
重力的方向竖直向下，电场力方向只能向上，由于小球带正电，所以电场强度方向竖直向上。

(2)小球做匀速圆周运动，O′为圆心，MN为弦长，，如图所示。设半径为r，由几何关系知

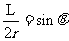
小球做匀速圆周运动的向心力由洛仑兹力提供，设小球做圆周运动的速率为v，有

由速度的合成与分解知

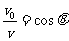
解得

(3)设小球到M点时的竖直分速度为vy，它与水平分速度的关系为

由匀变速直线运动规律

解得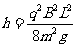

10.(2010·福建省龙岩模拟)如图所示，水平放置的平行金属板a、b带有等量异种电荷，a板带正电，两板间有垂直于纸面向里的匀强磁场，若一个带正电的液滴在两板间做直线运动其运动的方向是　　 (　 )

　　　 A．沿竖直方向向下　　　　　 B．沿竖直方向向上

　　　 C．沿水平方向向左　　 D．沿水平方向向右

[答案]D

[解析]一个带正电的液滴在两板间做直线运动，洛伦兹力与电场力重力平衡，洛伦兹力方向向上，根据左手定则，沿直线运动水平方向向右运动，D正确.

9.(2010·重庆南开中学高6月考前模拟测试卷)如题图所示，M、N为两块带等量异种电荷的平行金属板，板上有正对的小孔，N板右侧有两个宽度分别 为d和2d的匀强磁场区域，磁感应强度大小分别为2B和B，方向分别垂直于纸面向里和向外．板左侧电子经小孔O1进入两板间，O2在磁场边界上，O1 O2连线过板上正对的小孔且与磁场边界垂直，电子的质量为m，电荷量大小为e，电子重力和进入两板间初速度可以忽略．求：

(1)当两板间电势差为U0时，求从N板小孔射出的电子的速度v0；

(2)两金属板间电势差U在什么范围内，电子不能进入右侧磁场区域；

(3)如果电子从右边界的P点穿出，P与O2间距离为2d，求两金属板间电势差U大小。

[解析](1)根据动能定理，得(3分)　 解得

(2)欲使电子不能穿过磁场区域而打在荧光屏上，应有．

而由此即可解得

(3)若电子在左边磁场区域做圆周运动的轨道半径为rl，左边磁场区域做圆周运动的轨道半径为r2，有r2 = 2rl　

则由轨迹图几何关系可得

　即

解得 　

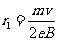注意到 　和 　　　　　

8.(2010·江苏省淮阴中学高三学情调研)如图所示，正方形区域abcd中充满匀强磁场，磁场方向垂直纸面向里。一个氢核从ad边的中点m沿着既垂直于ad边又垂直于磁场的方向，以一定速度射入磁场，正好从ab边中点n射出磁场。若将磁场的磁感应强度变为原来的2倍，其他条件不变，则这个氢核射出磁场的位置是

A．在b、n之间某点　　　　 B．在n、a之间某点

C．就从a点射出　　　　　　 D．在a、m之间某点

[答案]C

[解析]根据半径公式，磁感应强度变为原来的2倍，则半径变为原来的一半，粒子就从a点射出。

6.(2010吉林市5月质量检测)在某平面上有一半径为R的圆形区域，区域内外均有垂直于该平面的匀强磁场，圆外磁场范围足够大，已知两部分磁场方向相反且磁感应强度都为B，方向如图所示。现在圆形区域的边界上的A点有一个电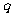量为，质量为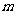的带电粒子以沿半径且垂直于磁场方向向圆外的速度经过该圆形边界，已知该粒子只受到磁场对它的作用力。

(1)若粒子在其与圆心O连线旋转一周时恰好能回到A点，试求该粒子运动速度V的可能值。

(2)在粒子恰能回到A点的情况下，求该粒子回到A点

所需的最短时间。

[解析](1)粒子运动的半径为r

BqV=m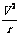

r=

如图，O1为粒子运动的第一段圆弧AB的圆心，

O2为粒子运动的第二段圆弧BC的圆心，

根据几何关系可知

tanθ=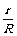

∠AOB=∠BOC=2θ

如果粒子回到A点，则必有

n×2θ=2π，n取正整数

可得

V=

考虑到θ为锐角，即0<θ<，根据③可得

n≥3 (2分)

故V=，(n=3，4，5……)

(2)粒子做圆周运动的周期

T=

因为粒子每次在圆形区域外运动的时间和圆形区域内运动的时间互补为一个周期T，所以粒子穿越圆形边界的次数越少，所花时间就越短，因此取n=3

可得

θ=　 　

而粒子在圆形区域外运动的圆弧的圆心角为α

α=2π-2(-θ)=

故所求的粒子回到A点的最短运动时间

t=T+T=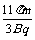 　

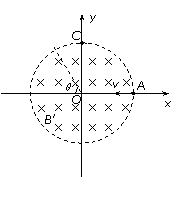　7.(2010·湖南省长沙市一中·雅礼中学高三三月联考)如图所示，在以直角坐标系xOy的坐标原点O为圆心、半径为r的圆形区域内，存在磁感应强度大小为B、方向垂直xOy所在平面的匀强磁场。一带电粒子由磁场边界与x轴的交点A处，以速度v0沿x轴负方向射入磁场，粒子恰好能从磁场边界与y轴的交点C处，沿y轴正方向飞出磁场，不计带电粒子所受重力。

(1)求粒子的荷质比。

(2)若磁场的方向和所在空间的范围不变，而磁感应强度的大小变为B′，该粒子仍从A处以相同的速度射入磁场，粒子飞出磁场时速度的方向相对于入射方向改变了θ角，求磁感应强度B′的大小。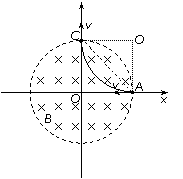

[解析](1)由几何关系可知，粒子的运动轨迹如图，其半径R=r，

洛伦兹力等于向心力，即

得　　　 　

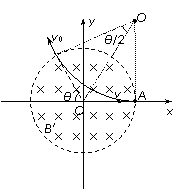(2)粒子的运动轨迹如图，设其半径为R′，洛伦兹力提供向心力，即

又因为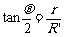　　　　 　

解得　　　　　 　

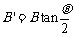
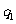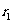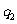5.(2010·山东省兖州市高三3月检测)一束带电粒子以同一速度，并从同一位置进入匀强磁场，在磁场中它们的轨迹如图所示．粒子的轨迹半径为，粒子的轨迹半径为，且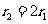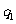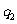，、分别是它们的带电量，则　　　　　　　 (　 )

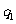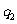A．带负电、带正电，荷质比之比为

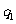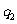B．带负电、带正电，荷质比之比为

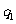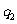C．带正电、带负电，荷质比之比为

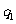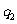D．带正电、带负电，荷质比之比为

[答案]C　

[解析]根据左手定则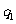，带正电、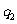带负电，根据半径公式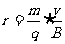荷质比之比为

4.(2010·海南省海口市高三调研测试)如图所示,一束电子以大小不同的速率沿图示方向飞入横截面为一正方形的匀强磁场区,在从ab边离开磁场的电子中，下列判断正确的是　　　　　　　　　　　　　

A.从b点离开的电子速度最大

B.从b点离开的电子在磁场中运动时间最长

C.从b点离开的电子速度偏转角最大

D.在磁场中运动时间相同的电子,其轨迹线一定重合

[答案]AD

[解析]从b点离开的电子轨道半径最大，根据半径公式，速度最大，A正确；从b点离开的电子圆心角等于900，时间为半周期，B、C错误；在磁场中运动时间相同的电子，其弧长一定相等，轨迹线一定重合，D正确

3.(2010·江苏省黄桥高三月考)如图所示，光滑的平行导轨倾角为θ，处在磁感应强度为 B 的匀强磁场中，导轨中接入电动势为E、内阻为r的直流电源，一阻值为R的电阻串联在电路中，电路中其余电阻不计，将质量为 m、长度为 L 的导体棒由静止释放，求导体棒在释放时的瞬时加速度的大小。

[解析] 导 体 棒 受 重 力 mg，支 持 力 N和安培力F，如图　 所 示，根 据牛顿第二定律，有

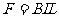
解得

2.(2010·福建省泉州市四校高三5月联考)如图所示，倾角为α的斜面上放有一通电的矩形线圈，电流方向沿adcba，线圈的ad边和bc边处于水平方向若整个装置放在一个磁场方向竖直向上的匀强磁场之中，线圈处于平衡状态，则()

A线圈的ad边所受斜面支持力比bc边大

B线圈的ab边和cd边不受磁场力作用

C线圈所受斜面摩擦力的方向沿斜面向上

D线圈所受斜面摩擦力比不存在磁场力大

[答案]AC

[解析]ad边和cd边所受安培力的方向分别为水平向内和水平向外，所以A正确。这两个力沿斜面方向的分力大小相等，方向相反，所以，沿斜面方向上线圈整体所受到的磁场作用力等于零，因此C正确，D错误。