11.(2010·闸北区高三年级物理学科期末)如图甲所示，一边长为L＝2.5m、质量为m＝0.5kg的正方形金属线框，放在光滑绝缘的水平面上，整个装置放在方向竖直向上、磁感应强度为B＝0.8T的有界匀强磁场中，它的一边与磁场的边界MN重合。在水平向左的力F作用下由静止开始向左运动，经过5s线框被拉出磁场。测得金属线框中的电流随时间变化的图像如图乙所示，在金属线框被拉出的过程中：

(1)求通过线框导线截面的电量及线框的电阻；

(2)写出水平力F随时间变化的表达式；

(3)已知在这5s内力F做功为1.92J，那么在此过程中，线框产生的焦耳热是多少？

[解析](1)根据q＝t，由I－t图像得：q＝1.25C

又根据

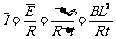
得

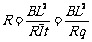＝4W

(2)由电流图像可知，感应电流随时间变化的规律：I＝0.1t

安培力FA＝BIL＝0.2t

由感应电流I＝，可得金属框的速度随时间也是线性变化的，v＝＝0.2t

线框做匀加速直线运动，加速度a＝0.2m/s2　

线框在外力F和安培力FA作用下做匀加速直线运动，F－FA＝ma

得力F＝(0.2t+0.1)N　

(3)t＝5s时，线框从磁场中拉出时的速度v5＝at＝1m/s

线框中产生的焦耳热Q＝W－mv52＝1.67J

10.(2010上海杨浦区期末)如图所示，一对平行光滑轨道放置在水平面上，两轨道相距L=1m，两轨道之间用电阻R=2Ω连接，有一质量为m=0.5kg的导体杆静止地放在轨道上与两轨道垂直，杆及轨道的电阻皆可忽略不计，整个装置处于磁感应强度B=2T的匀强磁场中，磁场方向垂直轨道平面向上．现用水平拉力沿轨道方向拉导体杆，使导体杆从静止开始做匀加速运动．经过位移s=0.5m后，撤去拉力，导体杆又滑行了相同的位移s后停下．

求：(1)全过程中通过电阻R的电荷量；

(2)匀加速运动的加速度；

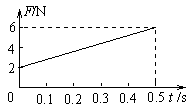
(3)画出拉力随时间变化的F-t图象．

[解析](1)设全过程中平均感应电动势为E，平均感应电流为I，时间，则通过电阻R的电荷量：

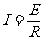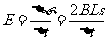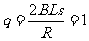q=I，， ．得C

　(2)拉力撤去时，导体杆的速度为v，拉力撤去后杆运动时间为，平均感应电流为I2，根据牛顿第二定律有：

，

∵　 ∴，

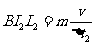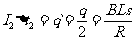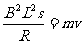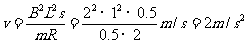
　 所以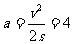m/s2

(3)，

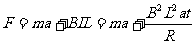拉力作用时间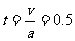s，此时Fmax=6N；

t = 0时，F=ma=2N

画出拉力随时间变化的F-t图象

9.(2010·汕头市高三5月教学质量测评 )如图所示，两根平行金属导轨固定在同一水平面内，间距为l，导轨左端连接一个电阻．一根质量为m、电阻为r的金属杆ab垂直放置在导轨上．在杆的右方距杆为d处有一个匀强磁场，磁场方向垂直于轨道平面向下，磁感应强度为B．对杆施加一个大小为F、方向平行于导轨的恒力，使杆从静止开始运动，已知杆到达磁场区域时速度为v，之后进入磁场恰好做匀速运动．不计导轨的电阻，假定导轨与杆之间存在恒定的阻力．求：

(1)导轨对杆ab的阻力大小f．

(2)杆ab中通过的电流及其方向．

(3)导轨左端所接电阻的阻值R．

[解析](1)杆进入磁场前做匀加速运动，有

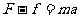
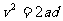
解得导轨对杆的阻力

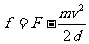
(2)杆进入磁场后做匀速运动，有

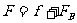
杆ab所受的安培力

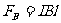
解得杆ab中通过的电流

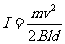
杆中的电流方向自a流向b　

(3)杆产生的感应电动势

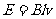
杆中的感应电流

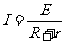
解得导轨左端所接电阻阻值

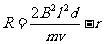
8.(2010年 惠州第三次调研)如图所示，两块水平放置的金属板距离为d，用导线、电键K与一个n匝的线圈连接，线圈置于方向竖直向上的均匀变化的磁场B中.两板间放一台小压力传感器，压力传感器上表面绝缘，在其上表面静止放置一个质量为m、电量为+q的小球.K断开时传感器上有示数，K闭合时传感器上的示数变为原来的一半.则线圈中磁场B的变化情况和磁通量变化率分别是　

A．磁场B正在增强　　

B．磁场B正在减弱

C．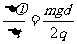　　

D．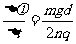

[答案]AD

[解析]闭合时传感器上的示数变小，说明上极板带负电，根据楞次定律，说明磁场正在增强，A正确，法拉第电磁感应定律，极板间电压为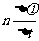，内部场强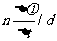，由于电场力等于重力的一半，所以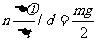，C正确

7.(天津市红桥区2010届高三二模)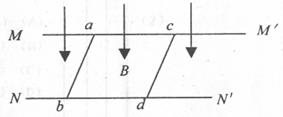如图所示，两条无限长且光滑的平行金属导轨的电阻为零，相距l=0．4m，水平放置在方向竖直向下、磁感应强度B=0．5T的匀强磁场中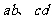，两金属棒长度与导轨宽度相同，电阻均为R=0．5 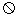，垂直地跨放在导轨上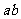，的质最为m1=0.4kg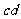，的质量为m2=0．1 kg，开始将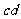棒锁定在导轨上，给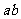棒一个向左的瞬时冲量，以初速度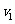5 m／s开始滑动，当速度降为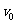=10 m／s时，将对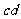棒的锁定解除。

(1)在解除对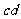棒的锁定前，电路中一共产生了多少焦耳热?

(2)在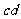刚开始运动时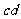，棒的加速度多大?

(3) 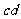棒能获得的最大速度是多大?

[解析](1)在解除对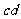棒的锁定前，电路中产生的焦耳热为

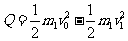
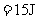
(2)在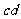刚开始运动时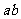，棒产生的感应电动势为

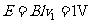
回路中的感应电流为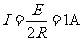

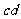棒受到的安培力为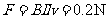

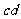棒的加速度大小为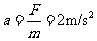

(3)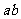棒和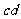棒组成的系统水平方向动量守恒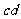，棒的最大速度为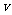,则

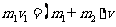
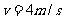
6.(2010北京西城区二模)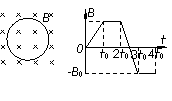如图所示，一闭合金属圆环处在垂直圆环平面的匀强磁场中。若磁感应强度B随时间t按如图所示的规律变化，设图中磁感应强度垂直纸面向里为正方向，环中感应电流沿顺时针方向为正方向，则环中电流随时间变化的图象是

[答案]D

[解析]0-t0阶段，正方向磁场均匀增加，根据法拉第电磁感应定律，电路中感应电流恒定，根据楞次定律，电路中感应电流方向逆时针；t0-2t0阶段，磁场不变，根据法拉第电磁感应定律，电路中电流为零，2t0-3t0阶段，正方向磁场均匀减小，负方向磁场均匀增加，但是变化率不变，根据法拉第电磁感应定律，电路中感应电流恒定，根据楞次定律，电路中感应电流方向顺时针，3t0-4t0阶段，磁场不变，根据法拉第电磁感应定律，电路中电流为零。所以D正确.

5.(2010上海虹口区4月模拟)如图所示，空间等间距分布着水平方向的条形匀强磁场，竖直方向磁场区域足够长，磁感应强度B＝1T，每一条形磁场区域的宽度及相邻条形磁场区域的间距均为d=0.5m，现有一边长l=0.2m、质量m=0.1kg、电阻R＝0.1Ω的正方形线框MNOP以v0=7m/s的初速从左侧磁场边缘水平进入磁场，求:

(1)线框MN边刚进入磁场时受到安培力的大小F。

(2)若线框能穿过的条形磁场区域为n个，且n＞3，请用文字简答线框通过2d的水平距离过程中其水平方向上做什么运动。

(3)线框从刚进入磁场到开始竖直下落的过程中产生的焦耳热Q。

[解析]⑴线框MN边刚进入磁场时有：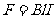　　 　

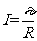
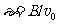
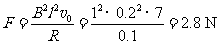
⑵线框通过2d的水平距离过程中其水平方向上分别做加速度减小的减速直线运动、匀速运动、加速度减小的减速直线运动、匀速运动。

⑶设线框竖直下落H时，速度为vH

由能量守恒得：　 )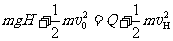

自由落体规律：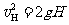

解得：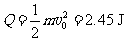

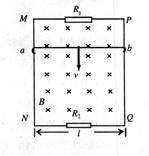
4.(2010北京宣武区一模)如图所示，MN和PQ为竖直方向的两平行长直金属导轨，间距l为0.40m，电阻不计. 导轨所在平面与磁感庆强度B=5.0T的匀强磁场垂直。质量m=6.0×10－2kg、电阻r=0.5Ω的金属杆ab始终垂直于导轨，并与其保持光滑接触。导轨两端分别接有阻值均为3.0Ω的电阻R1和R2。重力加速度取10m/s2，且导轨足够长，若使金属杆ab从静止开始下滑，求：

(1)杆下滑的最大速率vm；

(2)稳定后整个电路耗电的总功率P；

(3)杆下滑速度稳定之后电阻R2两端的电压U.

[解析](1)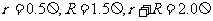

(2)由能量转化和守恒定律有：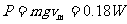

(3)

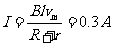
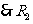两端的电压U=IR=0.45V

3.(2010上海徐汇区模拟)如图所示，两根竖直平行放置的光滑金属导轨相距为L，中间接有一阻值为R的定值电阻，在两导轨间abdc矩形区域内分布有磁感应强度为B的匀强磁场，磁场方向垂直导轨平面向里，宽度为d。一质量为m，电阻为r的导体棒MN垂直搁在导轨上，与磁场上边边界相距d0。现使棒MN由静止开始释放，当MN最终离开磁场前已开始做匀速直线运动，导轨电阻不计，棒下落过程中始终保持水平，并与导轨接触良好。

(1)求MN在离开磁场下边界时的速度大小；

(2)在通过磁场区域的过程中，求电流所做的功；

(3)试分析讨论棒在磁场中各种可能出现的运动情况及其对应的条件。

[解析](1)设MN离开磁场边界前做匀速运动的速度为v，产生的电动势为E = BLv

电路中电流 I = 　

对MN，由平衡条件得 mg－BIL = 0 (1分)　　 解得 v =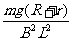 　

(2)由能量守恒定律：mg(d0 + d) = W电+ 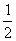mv2

解得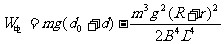 　

(3)设棒刚进入磁场时的速度为v0，由mgd0 = 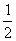mv02，得v0 =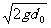 　

棒在磁场中匀速时速度为v = 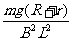，则

①当v0=v，即d0 = 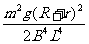时，棒进入磁场后即开始做匀速直线运动 　

②当v0 < v，即d0 <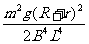时，棒进入磁场后做先加速后匀速直线运动

③ 当v0＞v，即d0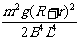＞时，棒进入磁场后做先减速后匀速直线运动

2.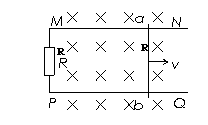(2010年惠州第三次调研)如下图所示，MN、PQ是间距为L的平行金属导轨，置于磁感强度为B，方向垂直导轨所在平面向里的匀强磁场中，M、P间接有一阻值为R的电阻．一根与导轨接触良好、有效阻值为R/2的金属导线ab垂直导轨放置，并在水平外力F的作用下以速度v向右匀速运动，则(不计导轨电阻)　

A．通过电阻R的电流方向为P-R-M

B．ab两点间的电压为BLv

C．a端电势比b端高

D．外力F做的功等于电阻R上发出的焦耳热

[答案]C

[解析]MN相当于电源，ab两点间的电压为路端电压，小于电源的电动势，B错误；根据右手定则，a相当于电源的正极，C正确；通过电阻R的电流方向为M-R-P，A错误；外力F做的功等于电路中总电阻发出的焦耳热，D错误。