
5.(2004年高考数学江苏卷,1)设集合P={1,2,3,4},Q={ },则P∩Q等于 ( )
},则P∩Q等于 ( )
A.{1,2} B. {3,4} C. {1} D. {-2,-1,0,1,2}
答案:A
4.(2004年高考数学广西卷,19)某村计划建造一个室内面积为800 的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3 宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
分析:本小题主要考查把实际问题抽象为数学问题,应用不等式等基础知识和方法解决问题的能力.
解:设矩形温室的左侧边长为a m,后侧边长为b m,则 ab=800.
蔬菜的种植面积 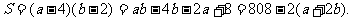
所以 
当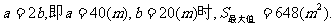
答:当矩形温室的左侧边长为40m,后侧边长为20m时,蔬菜的种植面积最大,最大种植面积为648m2.
3.(2004年高考数学广西卷,11)设函数 ,则使得
,则使得 的自变量
的自变量 的取值范围为
(
)
的取值范围为
(
)
A. B.
B.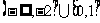
C. 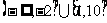 D.
D.
答案:A
2.(2004年高考数学广西卷,8)不等式 的解集为 ( )
的解集为 ( )
A.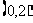 B.
B.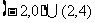 C.
C. D.
D.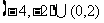
答案:D
1.(2004年高考数学广西卷,5)函数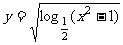 的定义域为( )
的定义域为( )
A. B.
B.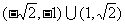
C.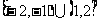 D.
D.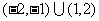
答案:A
9.注意事项:
⑴解不等式的基本思想是转化、化归,一般都转化为最简单的一元一次不等式(组)或一元二次不等式(组)来求解,。
⑵解含参数不等式时,要特别注意数形结合思想,函数与方程思想,分类讨论思想的录活运用。
⑶不等式证明方法有多种,既要注意到各种证法的适用范围,又要注意在掌握常规证法的基础上,选用一些特殊技巧。如运用放缩法证明不等式时要注意调整放缩的度。
⑷根据题目结构特点,执果索因,往往是有效的思维方法。
(Ⅱ)2004年高考数学不等式综合题选
8.不等式应用问题体现了一定的综合性.这类问题大致可以分为两类:一类是建立不等式、解不等式;另一类是建立函数式求最大值或最小值.利用平均值不等式求函数的最值时,要特别注意“正数、定值和相等”三个条件缺一不可,有时需要适当拼凑,使之符合这三个条件.利用不等式解应用题的基本步骤:10审题,20建立不等式模型,30解数学问题,40作答。
7.不等式这部分知识,渗透在中学数学各个分支中,有着十分广泛的应用.因此不等式应用问题体现了一定的综合性、灵活多样性,这对同学们将所学数学各部分知识融会贯通,起到了很好的促进作用.在解决问题时,要依据题设、题断的结构特点、内在联系、选择适当的解决方案,最终归结为不等式的求解或证明.不等式的应用范围十分广泛,它始终贯串在整个中学数学之中.诸如集合问题,方程(组)的解的讨论,函数单调性的研究,函数定义域的确定,三角、数列、复数、立体几何、解析几何中的最大值、最小值问题,无一不与不等式有着密切的联系,许多问题,最终都可归结为不等式的求解或证明。
6.证明不等式的方法灵活多样,但比较法、综合法、分析法和数学归纳法仍是证明不等式的
基本方法.要依据题设、题断的结构特点、内在联系,选择适当的证明方法,要熟悉各种证法中的推理思维,并掌握相应的步骤,技巧和语言特点.
5.证明不等式的方法灵活多样,内容丰富、技巧性较强,这对发展分析综合能力、正逆思维
等,将会起到很好的促进作用.在证明不等式前,要依据题设和待证不等式的结构特点、内在联系,选择适当的证明方法.通过等式或不等式的运算,将待证的不等式化为明显的、熟知的不等式,从而使原不等式得到证明;反之亦可从明显的、熟知的不等式入手,经过一系列的运算而导出待证的不等式,前者是“执果索因”,后者是“由因导果”,为沟通联系的途径,证明时往往联合使用分析综合法,两面夹击,相辅相成,达到欲证的目的.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com