
4.解:因为随机变量的概率非负且随机变量取遍所有可能值时相应的概率之和等于1,所以 解得
解得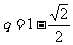 。
。
三解答题:
1.答案: 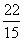 ; 2.答案:
; 2.答案: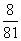
3. 答案: 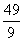 解析:投两个骰子共有36种可能,即
解析:投两个骰子共有36种可能,即
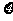 1 12 |
1 |
2 |
2 |
3 |
3 |
3 |
|
1 2 2 3 3 3 |
1 2 2 3 3 3 |
2 4 4 6 6 6 |
2 4 4 6 6 6 |
3 6 6 9 9 9 |
3 6 6 9 9 9 |
3 6 6 9 9 9 |
∴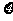 的分布列为
的分布列为
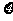 |
1 |
2 |
3 |
4 |
6 |
9 |
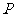 |
 |
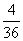 |
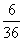 |
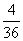 |
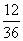 |
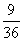 |
∴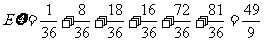
4. 答案:B 解析:这里的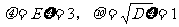 ;由换算关系式
;由换算关系式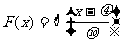 ,有
,有
 5.答案:C 6.答案:C
5.答案:C 6.答案:C
二填空题:
3.答案:由已知得 即
即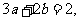
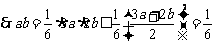 ,故选D.
,故选D.
2.答案:D解析:设二级品有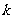 个,∴ 一级品有
个,∴ 一级品有 个,三级品有
个,三级品有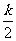 个,总数为
个,总数为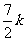 个。
个。
∴ 分布列为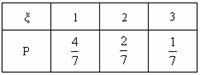
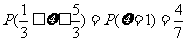
1. 答案:B;[解题思路]: 由离散型随机变量分布列的性质可得
解析:由
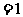 ,又
,又
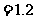 ,可得
,可得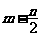
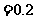
[名师指引]离散型随机变量的分布列都具有下面两个性质:
⑴Pi≥0,i=1,2,…;
⑵P1+P2+…=1.
2. 甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲面试合格的概率为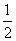 ,乙、丙面试合格的概率都是
,乙、丙面试合格的概率都是 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率; (2)签约人数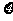 的分布列和数学期望.
的分布列和数学期望.
高三数学章节训练题28《随机变量及其分布》答案
1. 若随机事件A在1次试验中发生的概率是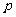 ,用随机变量
,用随机变量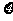 表示A在1次实验中发生的次数。(1)求方差
表示A在1次实验中发生的次数。(1)求方差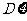 的最大值;(2)求
的最大值;(2)求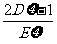 的最大值.
的最大值.
4. 设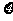 是一个离散型随机变量,其分布列如下表,则
是一个离散型随机变量,其分布列如下表,则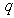 =
.
=
.
 |
-1 |
0 |
1 |
|
P |
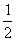 |
1-2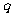 |
 |
3. 同时掷两枚骰子,它们各面分别刻有: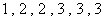 ,若
,若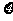 为掷得点数之积,则
为掷得点数之积,则 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com