
2.(本题满分14分)已知函数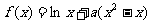
(I)若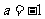 时,求
时,求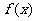 的极值;
的极值;
(Ⅱ)若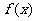 存在的单调递减区间,求
存在的单调递减区间,求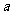 的取值范围;
的取值范围;
(Ⅲ)若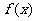 图象与
图象与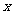 轴交于
轴交于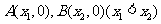 ,
,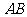 的中点为
的中点为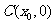 ,求证:
,求证: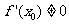
1.(本题满分14分)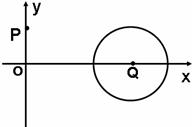 在平面直角坐标系
在平面直角坐标系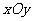 中,已知圆
中,已知圆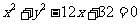 的圆心为
的圆心为 ,过点
,过点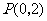 且斜率为
且斜率为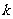 的直线与圆
的直线与圆 相交于不同的两点
相交于不同的两点 .
.
(Ⅰ)求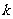 的取值范围;
的取值范围;
(Ⅱ)是否存在常数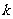 ,使得向量
,使得向量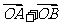 与
与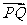 共线?如果存在,求
共线?如果存在,求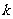 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
3.解:(本小题满分14分 

(1)
设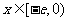 ,则
,则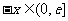 ,所以
,所以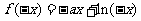
又因为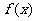 是定义在
是定义在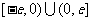 上的奇函数,所以
上的奇函数,所以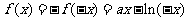
故函数 的解析式为
的解析式为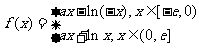 …………………4分
…………………4分
(2)证明:当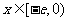 且
且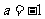 时,
时, ,设
,设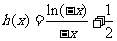
因为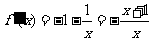 ,所以当
,所以当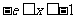 时,
时,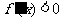 ,此时
,此时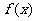 单调递减;当
单调递减;当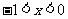 时,
时,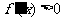 ,此时
,此时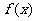 单调递增,所以
单调递增,所以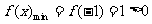
又因为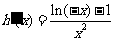 ,所以当
,所以当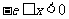 时,
时,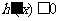 ,此时
,此时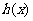 单调递减,所以
单调递减,所以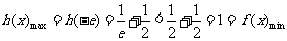


所以当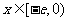 时,
时,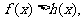 即
即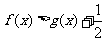 ……………………8分
……………………8分
(3)解:假设存在实数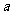 ,使得当
,使得当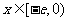 时,
时,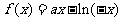 有最小值是3,则
有最小值是3,则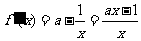
(ⅰ)当 ,
,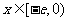 时,
时,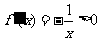 .
.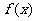 在区间
在区间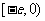 上单调递增,
上单调递增,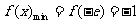 ,不满足最小值是3
,不满足最小值是3
(ⅱ)当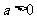 ,
,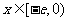 时,
时,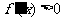 ,
,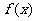 在区间
在区间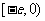 上单调递增,
上单调递增,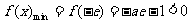 ,也不满足最小值是3
,也不满足最小值是3
(ⅲ)当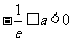 ,由于
,由于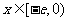 ,则
,则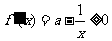 ,故函数
,故函数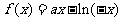 是
是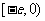 上的增函数.
上的增函数.
所以 ,解得
,解得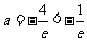 (舍去)
(舍去) 

(ⅳ)当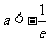 时,则
时,则
当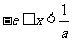 时,
时,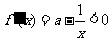 ,此时函数
,此时函数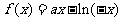 是减函数;
是减函数;
当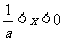 时,
时,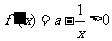 ,此时函数
,此时函数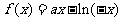 是增函数.
是增函数.
所以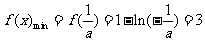 ,解得
,解得


综上可知,存在实数 ,使得当
,使得当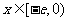 时,
时,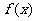 有最小值3…………14分
有最小值3…………14分
2、解:(1)由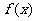 =
=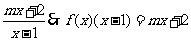 .
.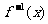 =
=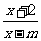 ,∴
,∴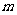 =1;…4分
=1;…4分
(2)任取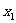 、
、 ∈(1,+∞),且设
∈(1,+∞),且设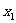 <
< ,则:
,则:
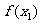 -
-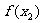 =
=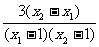 >0,
>0,


∴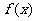 =
=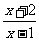 在(1,+∞)上是单调递减函数;…………………8分
在(1,+∞)上是单调递减函数;…………………8分
(3)当直线 =
=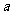 (
(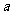 ∈R)与
∈R)与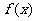 的图象无公共点时,
的图象无公共点时,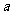 =1,
=1,
∴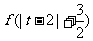 <2+
<2+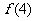 =4=
=4= ,|
,|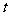 -2|+
-2|+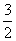 >2,
>2,
得: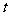 >
>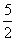 或
或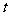 <
<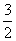 .
………12分
.
………12分
1.(1)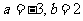
(2) ,
,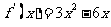



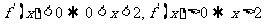
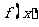 在
在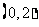 上单调递减,
上单调递减,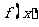 在
在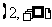 上单调递增。
上单调递增。
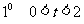 时,
时,
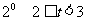 时,
时,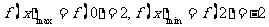 ;
;
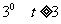 时,
时,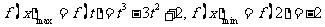
3.(14分)已知函数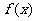 是定义在
是定义在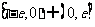 上的奇函数,当
上的奇函数,当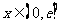 时,
时, 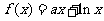 (其中e是自然对数的底,
(其中e是自然对数的底, 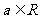 )
)


(1) 求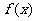 的解析式;
的解析式;
(2) 设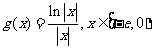 ,求证:当
,求证:当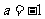 时,
时,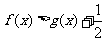 ;
;
(3)是否存在实数a,使得当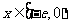 时,
时,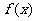 的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
2.(本题满分12分)设函数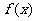 =
=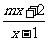 的图象的对称中心为点(1,1).
的图象的对称中心为点(1,1).
(1)求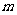 的值;
的值;
(2)判断并证明函数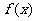 在区间(1,+∞)上的单调性;
在区间(1,+∞)上的单调性; 

(3)若直线 =
=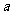 (
(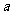 ∈R)与
∈R)与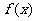 的图象无公共点,且
的图象无公共点,且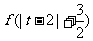 <2
<2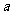 +
+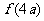 ,求实数
,求实数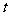 的取值范围.
的取值范围.
1.
(本题满分12分)已知函数1.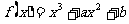 的图象在点P(1,0)处的切线与直线
的图象在点P(1,0)处的切线与直线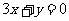 平行。
平行。
(1) 求常数a、b的值;
(2)
求函数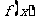 在区间
在区间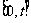 上的最小值和最大值(
上的最小值和最大值(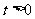 )。
)。
2. 解: 用A,B,C分别表示事件甲、乙、丙面试合格.由题意知A,B,C相互独立,
且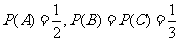 .------------------------------------------------------2分
.------------------------------------------------------2分
(1)至少有1人面试合格的概率是
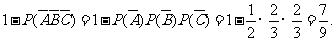 ----------------------4分
----------------------4分
(2)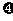 的可能取值为0,1,2,3.----------------------------------------------------------5分
的可能取值为0,1,2,3.----------------------------------------------------------5分
∵ 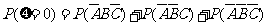
=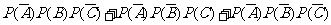
=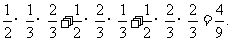 ---------------------------6分
---------------------------6分
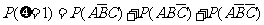
=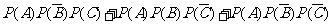
=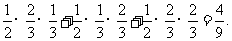 --------------------------------7分
--------------------------------7分
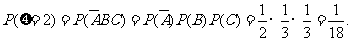 ---------------------8分
---------------------8分
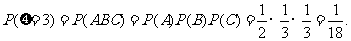 ----------------------9分
----------------------9分
∴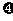 的分布列是
的分布列是
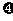 |
0 |
1 |
2 |
3 |
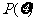 |
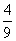 |
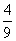 |
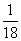 |
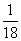 |
--------10分
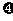 的期望
的期望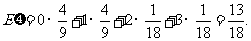 ----------------------------------------12分
----------------------------------------12分
1.[解题思路]:
(1)由两点分布,分布列易写出,而要求方差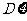 的最大值需求得
的最大值需求得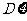 的表达式,转化为二次函数的最值问题;
的表达式,转化为二次函数的最值问题;
(2)得到 后自然会联想均值不等式求最值。
后自然会联想均值不等式求最值。
解析:(1)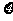 的分布列如表:所以
的分布列如表:所以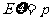 ,
,
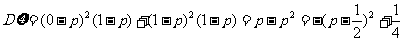
所以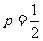 时,
时,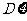 有最大值
有最大值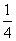 。
。
(2)由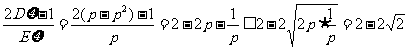 ,当且仅当
,当且仅当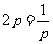 即
即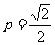 时取等号,所以
时取等号,所以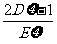 的最大值是
的最大值是 。
。
[名师指引]在超几何分布中,只要知道N,M和n,就可以根据公式求出X取不同m值时的概率P(X=m).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com