
1.(选修4-1:几何证明选讲)自圆O外一点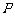 引切线与圆切于点
引切线与圆切于点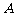 ,
, 为
为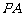 中点,过
中点,过 引割线交圆于
引割线交圆于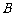 ,
,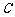 两点.求证:
两点.求证: .
.
20.已知关于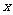 的函数
的函数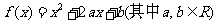
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)令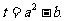 若存在实数
若存在实数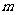 ,使得
,使得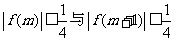 同时成立,求
同时成立,求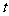 的最大值
的最大值
盐城中学2010届高三年级第一次模拟考试
数学试题
B.附加题部分
19.已知无穷数列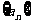 中,
中,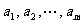 是首项为
是首项为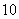 ,公差为
,公差为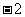 的等差数列;
的等差数列;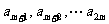 是首项为
是首项为 ,公比为
,公比为 的等比数列
的等比数列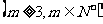 ,并对任意
,并对任意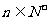 ,均有
,均有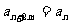 成立,
成立,
(Ⅰ)当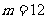 时,求
时,求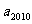 ;
;
(Ⅱ)若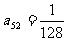 ,试求
,试求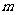 的值;
的值;
(Ⅲ)判断是否存在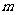 ,使
,使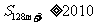 成立,若存在,求出
成立,若存在,求出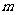 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
18.已知圆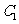 :
: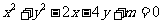 ,直线
,直线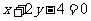 与圆
与圆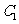 相交于
相交于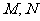 两点,以
两点,以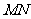 为直径作圆
为直径作圆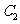 .
.
(Ⅰ)求圆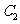 的圆心
的圆心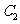 坐标;
坐标;
(Ⅱ)过原点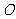 的直线
的直线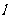 与圆
与圆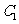 、圆
、圆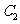 都相切,求直线
都相切,求直线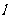 的方程.
的方程.
17.游泳池中相邻的两条泳道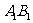 和
和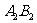 (看成两条互相平行的线段)分别长90米,甲在泳道
(看成两条互相平行的线段)分别长90米,甲在泳道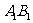 上从
上从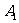 处出发,以
处出发,以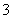 米/秒的速度到达
米/秒的速度到达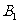 以同样的速度返回
以同样的速度返回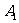 处,然后重复上述过程;乙在泳道
处,然后重复上述过程;乙在泳道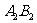 上从
上从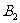 处出发,以
处出发,以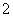 米/秒的速度到达
米/秒的速度到达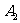 以同样的速度游回
以同样的速度游回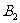 处,然后重复上述过程.(不考虑每次折返时的减速和转向时间).两人同时开始运动.
处,然后重复上述过程.(不考虑每次折返时的减速和转向时间).两人同时开始运动.
 (Ⅰ)设甲离开池边
(Ⅰ)设甲离开池边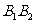 处的距离为
处的距离为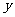 米,当时间
米,当时间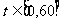 (单位:秒)时,写出
(单位:秒)时,写出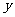 关于
关于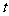 的函数解析式;
的函数解析式;
(Ⅱ)请判断从开始运动起到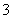 分钟为止,甲乙
的相遇次数.
分钟为止,甲乙
的相遇次数.
16.在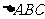 中,
中,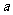 、
、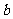 、
、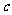 分别是角
分别是角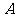 、
、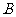 、
、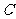 的对边,
的对边,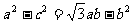 ,
, .
.
(Ⅰ)求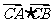 的值;
的值;
(Ⅱ)设函数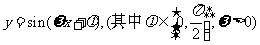 ,最小正周期为
,最小正周期为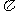 ,当
,当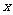 等于角
等于角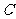 时函数取到最大值,求使该函数取最小值时的
时函数取到最大值,求使该函数取最小值时的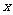 的集合.
的集合.
15.如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=1,D是BC的中点,点P在平面BCC1B1内,PB1=PC1=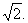 高.考.资.源.网
高.考.资.源.网
(Ⅰ)求证:PA1⊥BC;高.考.资.源.网
(Ⅱ)求证:PB1//平面AC1D.高.考.资.源.网
14.连续两次掷骰子得到的点数依次为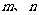 ,则以点
,则以点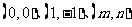 为顶点能构成直角三角形的概率为 ▲ .
为顶点能构成直角三角形的概率为 ▲ .
13.对于任意实数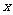 ,符号
,符号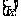 表示
表示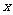 的整数部分,即
的整数部分,即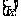 是不超过
是不超过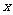 的最大整数.这个函数
的最大整数.这个函数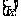 叫做“取整函数”,那么
叫做“取整函数”,那么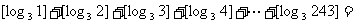 ▲ .
▲ .
12.已知数列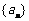 满足
满足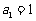 ,
,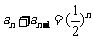
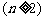 ,
,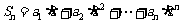 ,类比课本中推导等比数列前
,类比课本中推导等比数列前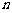 项和公式的方法,可求得
项和公式的方法,可求得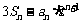 = ▲ .
= ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com