
(四)巩固练习:
1. 的解集是
的解集是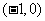 ;
;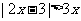 的解集是
的解集是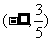 ;
;
2.不等式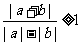 成立的充要条件是
成立的充要条件是 ;
;
3.若关于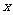 的不等式
的不等式 的解集不是空集,则
的解集不是空集,则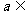
 ;
;
4.不等式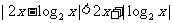 成立,则
成立,则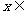

|

|
版权所有:()
版权所有:()
(三)例题分析:
例1.解下列不等式:
(1)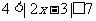 ;(2)
;(2) ;(3)
;(3)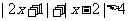 .
.
解:(1)原不等式可化为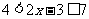 或
或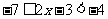 ,∴原不等式解集为
,∴原不等式解集为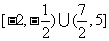 .
.
(2)原不等式可化为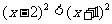 ,即
,即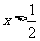 ,∴原不等式解集为
,∴原不等式解集为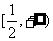 .
.
(3)当 时,原不等式可化为
时,原不等式可化为 ,∴
,∴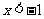 ,此时
,此时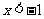 ;
;
当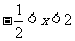 时,原不等式可化为
时,原不等式可化为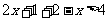 ,∴
,∴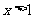 ,此时
,此时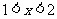 ;
;
当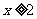 时,原不等式可化为
时,原不等式可化为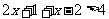 ,∴
,∴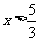 ,此时
,此时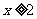 .
.
综上可得:原不等式的解集为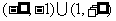 .
.
例2.(1)对任意实数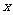 ,
,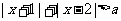 恒成立,则
恒成立,则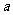 的取值范围是
的取值范围是 ;
;
(2)对任意实数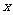 ,
,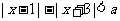 恒成立,则
恒成立,则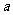 的取值范围是
的取值范围是 .
.
解:(1)可由绝对值的几何意义或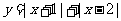 的图象或者绝对值不等式的性质
的图象或者绝对值不等式的性质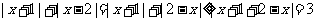 得
得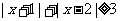 ,∴
,∴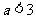 ;
;
(2)与(1)同理可得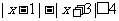 ,∴
,∴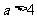 .
.
例3.(《高考 计划》考点3“智能训练第13题”)设
计划》考点3“智能训练第13题”)设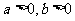 ,解关于
,解关于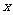 的不等式:
的不等式: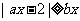 .
.
解:原不等式可化为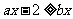 或
或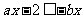 ,即
,即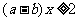 ①或
①或 ②,
②,
当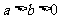 时,由①得
时,由①得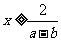 ,∴此时,原不等式解为:
,∴此时,原不等式解为: 或
或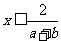 ;
;
当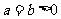 时,由①得
时,由①得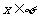 ,∴此时,原不等式解为:
,∴此时,原不等式解为: ;
;
当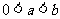 时,由①得
时,由①得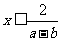 ,∴此时,原不等式解为:
,∴此时,原不等式解为: .
.
综上可得,当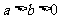 时,原不等式解集为
时,原不等式解集为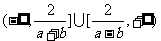 ,
,
当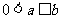 时,原不等式解集为
时,原不等式解集为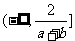 .
.
例4.已知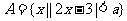 ,
,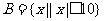 ,且
,且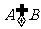 ,求实数
,求实数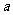 的取值范围.
的取值范围.
解:当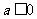 时,
时,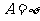 ,此时满足题意;
,此时满足题意;
当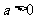 时,
时,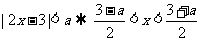 ,∵
,∵ ,
,
∴ ,
,
综上可得,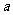 的取值范围为
的取值范围为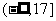 .
.
例5.(《高考 计划》考点3“智能训练第15题”)在一条公路上,每隔
计划》考点3“智能训练第15题”)在一条公路上,每隔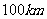 有个仓库(如下图),共有5个仓库.一号仓库存有
有个仓库(如下图),共有5个仓库.一号仓库存有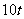 货物,二号仓库存
货物,二号仓库存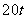 ,五号仓库存
,五号仓库存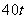 ,其余两个仓库是空的.现在想把所有的货物放在一个仓库里,如果每吨货物运输
,其余两个仓库是空的.现在想把所有的货物放在一个仓库里,如果每吨货物运输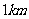 需要
需要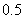 元运输费,那么最少要多少运费才行?
元运输费,那么最少要多少运费才行?

解:以一号仓库为原点建立坐标轴,
则五个点坐标分别为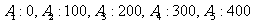 ,
,
设货物集中于点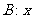 ,则所花的运费
,则所花的运费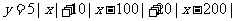 ,
,
当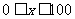 时,
时,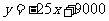 ,此时,当
,此时,当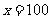 时,
时,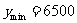 ;
;
当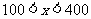 时,
时,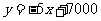 ,此时,
,此时,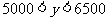 ;
;
当 时,
时,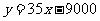 ,此时,当
,此时,当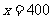 时,
时,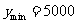 .
.
综上可得,当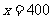 时,
时,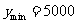 ,即将货物都运到五号仓库时,花费最少,为
,即将货物都运到五号仓库时,花费最少,为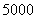 元.
元.
(二)主要方法:
1.解含绝对值的不等式的基本思想是去掉绝对值符号,将其等价转化为一元一次(二次)不等式(组)进行求解;
2.去掉绝对值的主要方法有:
(1)公式法: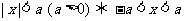 ,
,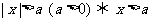 或
或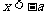 .
.
(2)定义法:零点分段法;
(3)平方法:不等式两边都是非负时,两边同时平方.
(一)主要知识:
1.绝对值的几何意义: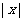 是指数轴上点
是指数轴上点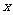 到原点的距离;
到原点的距离;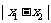 是指数轴上
是指数轴上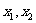 两点间的距离
两点间的距离
2.当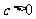 时,
时,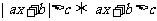 或
或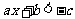 ,
,
 ;
;
当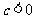 时,
时,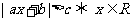 ,
,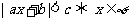 .
.
4、认真研读历届高考单项填空题并能举一反三
历年高考单项填空题考查虽各有所侧重,但万变不离其宗,认真研究历年高考单项填空题,会起到事半功倍的效果。
3、着重训练在具体的语境中灵活运用语言知识的能力高*考*资*源*网
近几年的高考单项填空题越来越重视情景的设置,复习时切忌只注重语言知识的识记而忽视其运用。
2、要重点突出,忌平均用力
动词是英语的核心,也是高考测试的重点。动词的时态、语态,非谓语动词,情态动词,连系动词,动词以及动词短语的辩义是复习的重点,特别要注意动词词义辨析,注意涉猎课外知识,增加动词在具体语言情景中的灵活运用。
1、全面牢固地掌握英语基础知识
高考英语单项填空题几乎覆盖了中学阶段所有的语言项目,因此同学们在进行复习时不要眼高手低,而应注重基础知识的掌握。切忌一味地搞偏难怪题,不切实际提高难度的做法是和高考的方向背道而驰的。
35. Alexander tried to get his work _______in the medical circles.
A. to recognize B. recognizing C. recognize D. recognized
[解析]D。考查非谓语动词。该题考查get后接复合宾语结构。句意为“Alexander努力让他的工作在医疗界得到任可。”作宾补的非谓语动词与其逻辑主语his work含有逻辑上的被动意义,故选择表示被动意义的过去分词作宾补。
2010年新课标全国卷单项填空题给我们的启示:高*考*资*源*网
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com