

19.某大学开设甲、乙、丙三门选修课 ,学生是否选修哪门课互不影响. 已知某学生只选修甲的概率为
,学生是否选修哪门课互不影响. 已知某学生只选修甲的概率为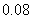 ,只选修甲和乙的概率是
,只选修甲和乙的概率是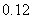 ,至少选修一门的概率是
,至少选修一门的概率是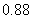 ,用
,用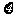 表示该学生选修的课程门数和没有选修的课程门数的乘积.
表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数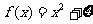
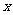 为
为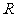 上的偶函数”为事件
上的偶函数”为事件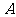 ,求事件
,求事件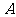 的概率;
的概率;
(2)求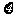 的分布列和数学期望.
的分布列和数学期望.
18.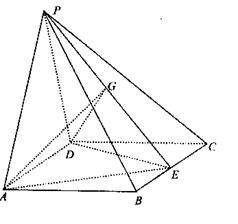 四棱锥P-ABCD中,侧面PAD
四棱锥P-ABCD中,侧面PAD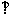 底面ABCD,底面ABCD是矩形,BC=2CD=2,又PA=PD,
底面ABCD,底面ABCD是矩形,BC=2CD=2,又PA=PD,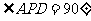 E、G分别是BC、PE的中点。
E、G分别是BC、PE的中点。
(1)求证:AD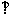 PE;
PE;
(2)求二面角E-AD-G的大小。
17.在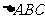 中,
中,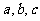 分别是角A、B、C的对边
分别是角A、B、C的对边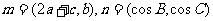 ,且
,且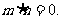
(1)求角B的大小;
(2)设函数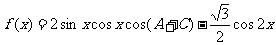 ,求函数
,求函数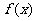 的最小正周期,最大值及当
的最小正周期,最大值及当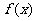 取得最大值时
取得最大值时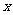
16.具有性质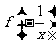 =
=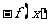 的函数,我们称其为满足“倒负”变换的函数,下列函数:
的函数,我们称其为满足“倒负”变换的函数,下列函数:
(1)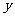 =
=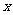 -
-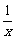
 ;(2)
;(2)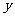 =
=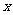 +
+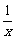 ;(3)
;(3)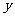 =
=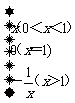 ,其中不满足“倒负”变换的函数是 .
,其中不满足“倒负”变换的函数是 .
15.如图,是某几何体的三视图,其中正视图是腰长为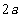 的等腰三角形俯视图是半径为
的等腰三角形俯视图是半径为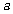 的半圆,则该几何体的表面积是
.
的半圆,则该几何体的表面积是
.

14.设0<θ<,已知a1=2cosθ,an+1=(n∈N+),猜想an=________.
13、按如图所示的程序框图运算,若输出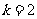 ,则输入
,则输入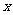 的取值范围是______
的取值范围是______
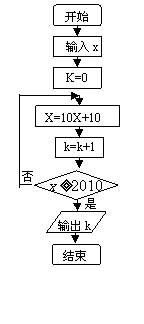

12.将一颗骰子投掷两次,第一次出现的点数记为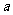 ,第二次出现的点数记为
,第二次出现的点数记为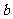 ,
,
设两条直线l1:ax+by=2,l2:x+2y=2平行的概率为P1,相交的概率为P2,试问点(P1,P2)与直线l2:x+2y=2的位置关系是 ( )
A.P在直线l2的右下方 B.P在l2直线的左下方
C.P在直线l2的右上方 D.P在直线l2上
11.设奇函数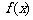 在
在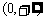 上是增函数,且
上是增函数,且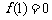 ,则不等式
,则不等式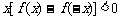 的解集为 ( )
的解集为 ( )
A.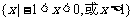 B.
B.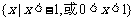
C.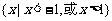
 D.
D.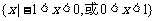
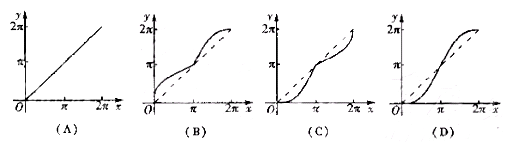
9.如图所示,单位圆中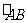 的长为
的长为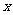 ,
,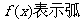
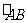 与弦AB所围成的弓
与弦AB所围成的弓
形面积的2倍, 则函数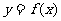 的图像是 ( )
的图像是 ( )
10.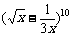 的展开式中含x的正整数指数幂的项数是 ( )
的展开式中含x的正整数指数幂的项数是 ( )
A.0 B.2 C.4 D.6
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com